Analizando el riesgo de una acción en R
Intro
En este tutorial vamos a cubrir lo siguiente:
Qué es el riesgo en inversiones
Cómo calcular varianza y desviación estándar
Cómo calcular medidas alternativas de riesgo
Qué es el CAPM y cómo se calcula la beta de una acción
1 ¿Qué es el riesgo?
Invertir es apostar al futuro. Todos nosotros compramos una acción, ETF, derivado, cryptomoneda, etc. con la esperanza de que su valor sea mayor en el futuro. Sin embargo, nadie conoce el futuro. De este simple hecho emana todo el riesgo posible. El riesgo es la posibilidad de que suceda un evento adverso a nuestra expectativa.
Existen muchísimas maneras de medir el riesgo, pero la más común es utilizando alguna medida de volatilidad. En este tutorial vamos a entender y calcular diferentes medidas de riesgo.
2 Varianza y desviación estándar
La varianza y la desviación estándar son las medidas más comunes cuando hablamos de volatilidad en las inversiones. La varianza se calcula de la siguiente manera:
var = (1/n) sum((x - mu)^2)
donde x es nuestra variable de interés
n es el número de observaciones de x
mu es la media de x En R es muy fácil de implementar:
my_var <- function(series) {
(1 / length(series)) * sum((series - mean(series))^2)
}Sin embargo, si creamos una variable aleatoria para probar nuestra función, nos damos cuenta que es diferente el valor que arroja nuestra función y la función var de R:
Esta discrepancia se debe a que R calcula lo que se llama “varianza de muestra” y nuestra fórmula está calculando lo que se llama “varianza de población”. El ajuste es muy sencillo, hay que restarle 1 a nuestro denominador:
my_var <- function(series) {
(1 / (length(series) - 1)) * sum((series - mean(series))^2)
}Esto nos da ahora sí exactamente el mismo resultado que la función var( ) de R:
Es importante que tengamos esto en cuenta. Es el mismo caso para la desviación estándar: la función sd( ) de R calcula la desviación estándar de muestra. Si queremos calcular la desviación estándar de población tendremos que hacer nuestra propia función. Para propósitos de este tutorial, la desviación estándar de muestra basta, así que no será necesario.
La desviación estándar es la raíz cuadrada de la varianza, por lo que podemos calcularla usando cualquiera de los siguientes comandos:
sd(x)
sqrt(var(x))Y podemos ver que el resultado es el mismo:
Cuando hablamos de activos financieros, lo que nos interesa es saber cuál es la volatilidad de sus retornos. Para esto, investigaremos la acción de ALFA para los últimos 10 años:
library(quantmod)
alfa <- na.omit(Ad(getSymbols("ALFAA.MX", from = "2011-10-19", auto.assign = FALSE)))
alfa_rets <- na.omit(dailyReturn(alfa, leading = FALSE))
sd(alfa_rets)Y obtenemos un valor de 2.20%:
Esta es la desviación estándar de los retornos diarios de ALFA. Se acostumbra que cuando hablamos de volatilidad usemos cifras anualizadas, así que hagamos eso:
sd(alfa_rets) * sqrt(252)Y obtenemos una volatilidad anualizada durante los últimos 10 años de 34.90%. El múltiplo de 252 viene de los 252 días hábiles en promedio que hay durante un año. Usamos la raíz cuadrada por que la desviación estándar no es aditiva (la varianza sí).
2.1 Usando PerformanceAnalytics
PerformanceAnalytics es uno de esos muchos paquetes que les comenté que podemos usar para aplicaciones de finanzas en R. Este paquete tiene una función muy útil para calcular la desviación estándar anualizada directamente:
StdDev.annualized(alfa_rets)Esta función nos arroja exactamente lo que habíamos calculado antes, 34.90%. Es especialmente útil cuando queremos calcular la desviación estándar de diferentes instrumentos al mismo tiempo. Vamos a calcular la desviación estándar de 3 acciones a continuación:
e <- new.env()
acciones <- c("ALFAA.MX", "CEMEXCPO.MX", "FEMSAUBD.MX")
getSymbols(acciones, env = e, from = "2011-10-19")
adj_ls <- lapply(e, Ad)
adj_prices <- na.omit(do.call(merge, adj_ls))
adj_rets <- na.omit(Return.calculate(adj_prices))
StdDev.annualized(adj_rets)Y podemos ver que CEMEX ha sido la acción más volátil de las 3 con una desviación estándar anualizada de 36.97% y FEMSA ha sido la menos volátil con 22.03%:
Si usamos la función sd( ) de R, verán que no obtenemos la volatilidad de cada columna sino del conjunto en general. Intenten usar sd( ) para obtener los mismos números que la función StdDev.annualized( ) (pista: usen la función apply( )).
2.2 Una advertencia sobre la desviación estándar
Aunque nos hemos concentrado por el momento en calcular desviación estándar y usar esto como nuestro indicador de riesgo, existen razones por las cuáles mucha gente no está de acuerdo con que la desviación estándar sea un indicador adecuado de riesgo. Uno de los argumentos va así: imagina que tienes un activo x y uno y. Los retornos diarios de ambos siguen una distribución normal de la siguiente forma: x ~ N(0.005, 0.2/sqrt(252)) y y ~ N(-0.005, 0.05/sqrt(252)). Aunque x sea más volátil que y, el activo x es sin lugar a dudas la mejor inversión:
x_rets <- rnorm(1000, mean = 0.005, sd = 0.2/sqrt(252))
y_rets <- rnorm(1000, mean = -0.005, sd = 0.05/sqrt(252))
crets_x <- cumprod(1 + x_rets) - 1
crets_y <- cumprod(1 + y_rets) - 1
par(mfrow = c(1, 2))
plot(crets_x, type = "l")
plot(crets_y, type = "l")Existen otras medidas que nos ayudan a calcular la probabilidad de perder dinero y no sólo la volatilidad de los retornos. A continuación veremos varios de ellos.
3 Medidas alternativas de riesgo
Como vimos anteriormente, a veces la desviación estándar de los retornos no es suficiente para caracterizar completamente el riesgo en una inversión. Vamos a ver a continuación 3 métricas adicionales que nos pueden ayudar.
3.1 Semidesviación y semivarianza
La semidesviación y semivarianza son muy similares. El punto es calcular la desviación estándar y varianza de un subconjunto de los retornos, generalmente los retornos negativos. En PerformanceAnalytics tenemos 2 funciones diferentes para calcular la semidesviación:
DownsideDeviation(adj_rets)
SemiDeviation(adj_rets)La diferencia entre las dos fórmulas es cuál es el threshold para el subconjunto de retornos. Con DownsideDeviation( ) el subconjunto son todos los retornos negativos, mientras que SemiDeviation( ) utiliza los retornos menores al retorno promedio de la muestra.
Para calcular semivarianza, eleva al cuadrado el resultado de cualquiera de estas dos. Existe una función SemiVariance( ) en PerformanceAnalytics, pero está calculando otra cosa (utilicen su conocimiento de RStudio para explorar las funciones del paquete y encuentren qué es lo que calcula esta función).
Antes de seguir con el resto de las medidas de riesgo alternativas, si quieren saber cual es la proporción de retornos negativos en la muestra, pueden usar la siguiente función:
DownsideFrequency(adj_rets)3.2 Drawdowns
El drawdown es la caída porcentual desde el último pico positivo de valor de un activo observado (también llamado ATH por las siglas en inglés de all time high). Si estamos en ATH, el drawdown es por definición 0. Si nuestro ATH es de $10 y en este momento el precio del activo es $9, nuestro drawdown es de -10%. Esta medida nos permite saber, desde su valor más alto, cuál es la caída más grande que ha tenido el activo que estemos analizando.
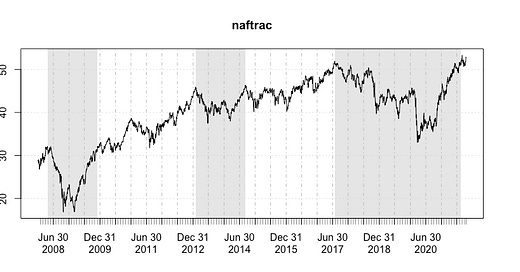
Analicemos los drawdowns del mercado mexicano. Para eso utilizaremos como proxy el ETF NAFTRAC:
naftrac <- na.omit(Ad(getSymbols("NAFTRAC.MX", auto.assign = FALSE)))
naftrac_rets <- na.omit(Return.calculate(naftrac))
chart.Drawdown(naftrac_rets)Podemos ver drawdowns significativos en 2008-2009, 2013-2014 y 2017-2021. Con funciones de PerformanceAnalytics podemos aislar los periodos exactos y crear una gráfica mejor. Usa los comandos a continuación e investiga cómo funciona cada uno:
naftrac_dd_info <- sortDrawdowns(findDrawdowns(naftrac_rets))
start_dates <- index(naftrac_rets)[naftrac_dd_info$from[1:3]]
end_dates <- index(naftrac_rets)[naftrac_dd_info$to[1:3]]
plot.xts(naftrac, blocks = list(start.time = start_dates, end.time = end_dates, col = "gray90"))Pasamos 4 años, desde julio de 2017 hasta agosto del 2021, sin avance en el índice bursátil más representativo de México.
3.3 VaR
El valor en riesgo (VaR por sus siglas en inglés) es la máxima pérdida posible para una inversión durante un periodo de tiempo definido con una probabilidad también definida. Por ejemplo, si un portafolio tiene un VaR diario de 5% de 1 millón de pesos, eso quiere decir que existe una probabilidad de 0.05 de que el portafolio pierda 1 millón de pesos en cualquier día. El VaR es muy común para temas regulatorios.
Existen 3 maneras principales de calcular el VaR:
VaR histórico: se escoge el cuantil correspondiente de la muestra de retornos históricos observados. Se usa cuando tienes una muestra suficientemente grande.
VaR paramétrico: se modela la distribución de retornos con alguna distribución de probabilidad (generalmente se utiliza la normal) y se calcula el VaR como el cuantil correspondiente de esta distribución calculada.
VaR modificado: debido al hecho de que los retornos de los instrumentos financieros no necesariamente siguen una distribución normal, esta versión del VaR utiliza la expansión de Cornish-Fisher para tomar en cuenta momentos superiores de la distribución (curtosis y skewness).
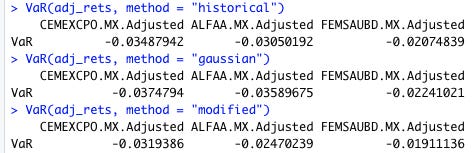
El paquete PerformanceAnalytics nos permite usar estas tres metodologías ajustando el paramentro method de la función VaR( ):
VaR(adj_rets, method = "historical")
VaR(adj_rets, method = "gaussian")
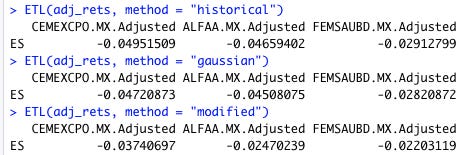
VaR(adj_rets, method = "modified")Una pregunta que probablemente se estén haciendo es, los días que sobrepase la pérdida del VaR, ¿cuánto voy a perder en promedio? Eso se conoce como expected shortfallı, conditional VaR, o simplemente CVaR. Por suerte, PerformanceAnalytics tiene la función ETL( ) disponible para responder esta pregunta:
ETL(adj_rets, method = "historical")
ETL(adj_rets, method = "gaussian")
ETL(adj_rets, method = "modified")Por definición, la pérdida calculada con CVaR siempre será mayor que la pérdida calculada con VaR, siempre y cuando se esté usando el mismo método para ambos.
4 El CAPM y la beta
El CAPM (por su nombre en inglés, capital asset pricing model) es un modelo usado para determinar el retorno esperado de un activo. Según este modelo, el retorno esperado de un activo está dado por la siguiente ecuación:
E(Ri) = Rf + B(E(Rm) - Rf)
donde E(Ri) es el retorno esperado para el activo
Rf es el retorno libre de riesgo
B es la beta del activo al mercado
E(Rm) es el retorno esperado del mercadoExisten 3 formas de calcular la beta en R:
Directamente con funciones de R
Con una regresión lineal
Con PerformanceAnalytics
Calculemos la beta de ALFA contra el mercado mexicano (usaremos NAFTRAC como proxy nuevamente). Primero bajamos los datos y calculamos los retornos necesarios:
e = new.env()
getSymbols(c("ALFAA.MX", "NAFTRAC.MX"), env = e)
adj_ls <- lapply(e, Ad)
adj_prices <- na.omit(do.call(merge, adj_ls))
adj_rets <- na.omit(Return.calculate(adj_prices))Ahora que ya tenemos los retornos de ALFA y del mercado, exploremos los 3 metodos que podemos utilizar para calcular la beta de ALFA:
cov(adj_rets$ALFAA.MX.Adjusted, adj_rets$NAFTRAC.MX.Adjusted) / var(adj_rets$NAFTRAC.MX.Adjusted)
capm <- lm(adj_rets$ALFAA.MX.Adjusted ~ adj_rets$NAFTRAC.MX.Adjusted)
coef(capm)[2]
CAPM.beta(adj_rets$ALFAA.MX.Adjusted, adj_rets$NAFTRAC.MX.Adjusted)El primer método es simplemente la covarianza de los retornos del activo y el mercado dividido por la varianza del mercado. El segundo método involucra llevar a cabo una regresión lineal, para la cual usamos la función lm( ) de R donde tienes que especificar la variable independiente (y) y dependiente (x) de la siguiente manera en el argumento de la función: y ~ x. Después con coef( ) extraemos los coeficientes de la regresión, el primero es el intercepto y el segundo es la beta, por eso especificamos que buscamos el segundo elemento. Por último, PerformanceAnalytics tiene la función CAPM.beta( ) para llevar a cabo este mismo cálculo.
Según el modelo CAPM entonces, por cada punto porcentual que suba el mercado, ALFA subirá 1.05%. Lo mismo es cierto a la baja, por cada punto que pierda el mercado, ALFA caerá 1.05%.
Ahora ya tienen herramientas para analizar el riesgo de una acción en R. Hasta el próximo tutorial!