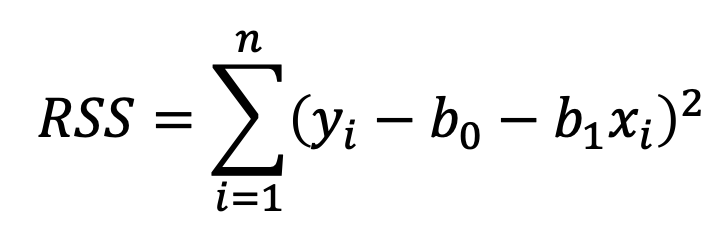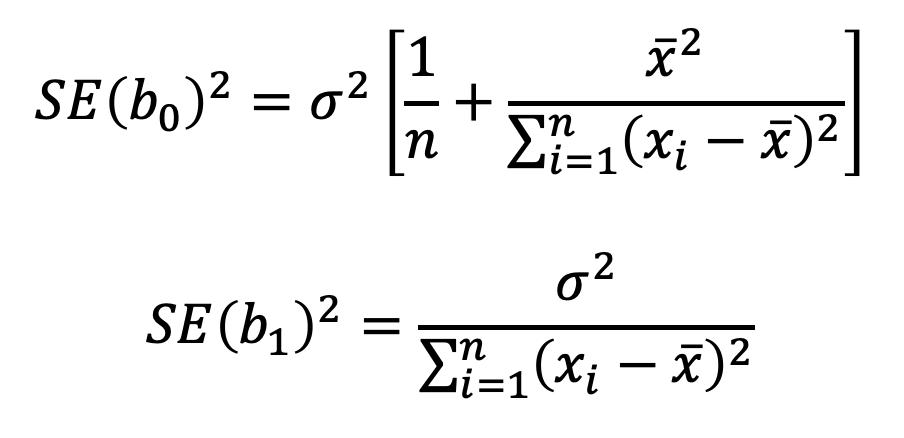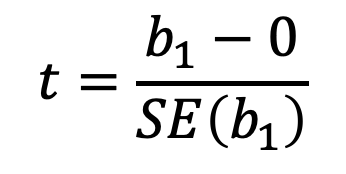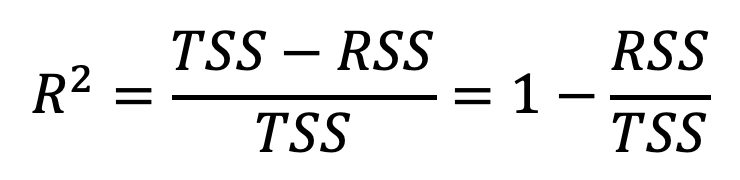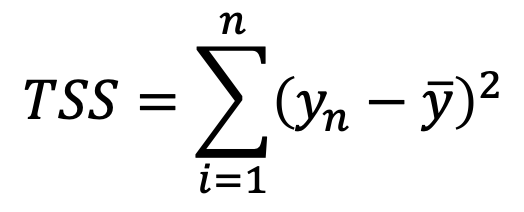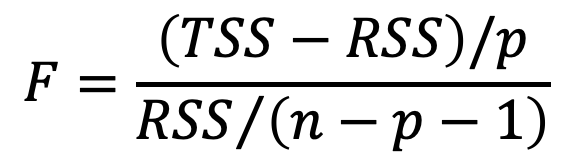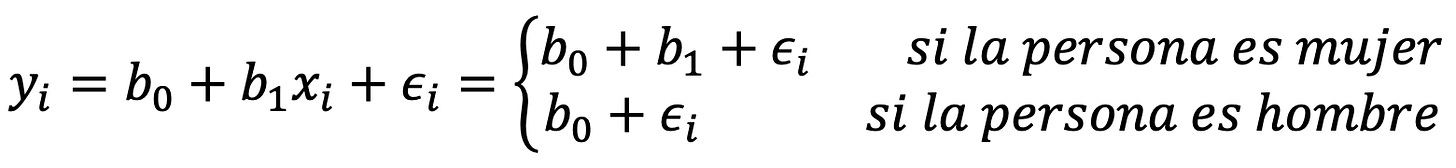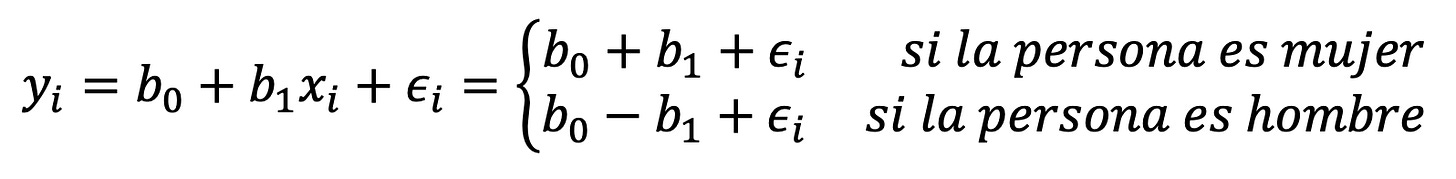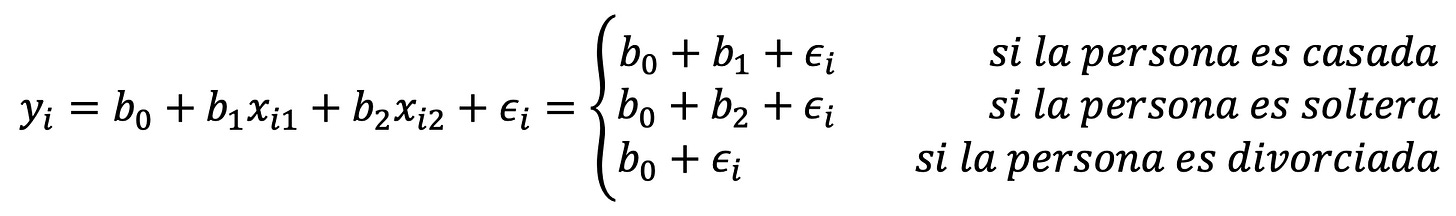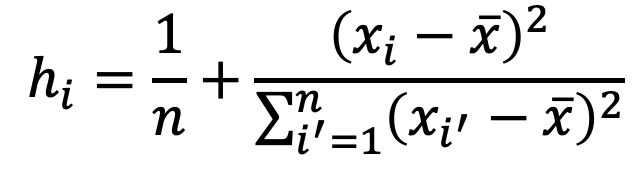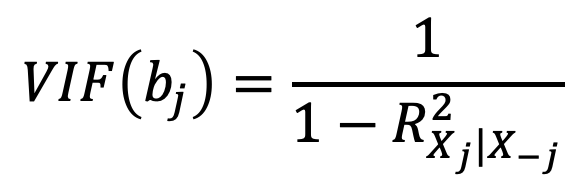Todo lo que necesitas saber sobre la regresión lineal
Intro
En este tutorial vamos a cubrir lo siguiente:
¿Qué es la regresión lineal?
Regresión lineal simple
Estimación de los coeficientes
Precisión de los coeficientes
Precisión del modelo
Regresión lineal múltiple
Estimación de coeficientes
Algunas notas importantes
Otras consideraciones del modelo
Predictores cualitativos
Extensiones del modelo lineal
Problemas potenciales
La respuesta a nuestras preguntas
Regresión lineal en R
1 ¿Qué es la regresión lineal?
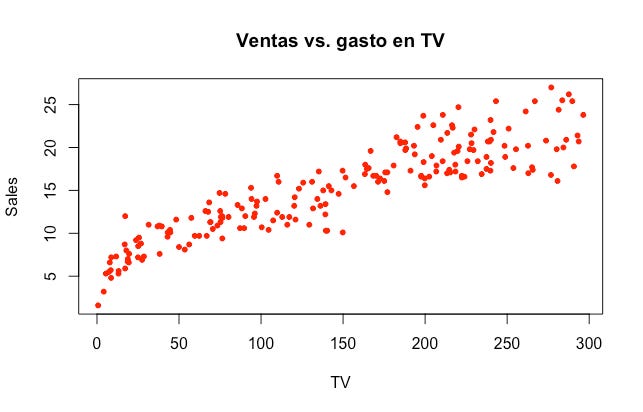
Recordemos el problema de la sección 2 del tutorial anterior. Yo quisiera contestar las siguientes preguntas respecto al efecto de los diferentes canales de publicidad sobre las ventas del producto:
¿Hay alguna relación entre el presupuesto de publicidad y las ventas?
Si sí, ¿qué tan fuerte es esta relación?
¿Qué canales contribuyen a las ventas?
¿De qué magnitud es el efecto de cada canal sobre las ventas?
¿Con qué grado de certeza podemos predecir ventas en el futuro?
La relación entre el presupuesto de publicidad y las ventas, ¿es lineal?
¿Existen sinergias entre los diferentes canales de publicidad?
La regresión lineal es un modelo que nos permite predecir una respuesta cuantitativa Y dependiendo de los predictores X. Vamos a conocer este procedimiento para poder responder las 7 preguntas anteriores.
2 Regresión lineal simple
En la regresión lineal simple, asumimos que existe sólo un predictor X que afecta la variable Y. Es decir:
Y ≅ b_0 + b_1*XEn este caso particular, una de las ecuaciones que podemos considerar sería:
ventas ≅ b_0 + b_1*TVY nuestro trabajo se resume a encontrar los b_0 y b_1 adecuados.
2.1 Estimación de los coeficientes
b_0 y b_1 son desconocidos. Nuestro objetivo es encontrar el par de coeficientes de manera que la ecuación se ajuste de manera razonable a los datos que hemos observado. La manera más común de encontrar estos parámetros es por el procedimiento de mínimos cuadrados ordinarios. Partiendo de los datos:
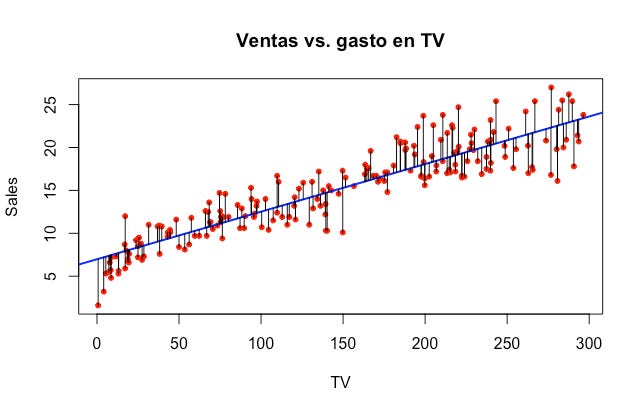
Nuestro objetivo es encontrar una línea recta que mejor se ajuste a los datos minimizando el cuadrado de la distancia entre la línea y cada punto:
Esta cantidad se conoce como la suma de los cuadrados de los residuales (RSS, por sus siglas en inglés):
A cada una de estas diferencias se le conoce como los residuales. En R vamos a encontrar los coeficientes con un solo comando rápidamente (más adelante veremos cómo hacer esto en R). Por ahora sólo tengan en mente que el objetivo es minimizar la ecuación anterior. Para nuestra muestra de ventas y gasto en TV, los números son los siguientes: b_0=6.9748 y b_1=0.0555.
2.2 Precisión de los coeficientes
Existe una manera de calcular que tan cerca están los b_0 y b_1 que estimamos anteriormente de los verdaderos b_0 y b_1 (que son desconocidos). Para eso necesitamos calcular el error estándar (SE, por sus siglas en inglés):
donde σ^2: Var(ϵ) (la varianza de los residuales)
n : número de observaciones de la respuesta YEstos errores estándar los utilizamos para calcular intervalos de confianza. Por ejemplo, en nuestro caso SE(b_0)=0.3226 y SE(b_1)=0.0019. Con un 95% de probabilidad, podemos afirmar que el verdadero b_0 y b_1 están entre los siguientes números:
En nuestro caso, b_0=[6.3387, 7.6109] y b_1=[0.0517, 0.0592]. Siempre y cuando el 0 no esté contenido en los intervalos, es señal de que vamos por buen camino. Si el 0 estuviera en los intervalos posibles, quiere decir que existe la posibilidad de que la relación entre X y Y no existe (b_1=0). Para determinar esto realizamos una prueba de hipótesis donde las hipótesis nula y alternativa son las siguientes:
H_0: No hay relación entre X y Y (o sea, b_1=0)
H_a: Hay alguna relación entre X y Y (o sea, b_1≠0)Si nuestro estimado de b_1 está suficientemente alejado de 0, podemos rechazar la hipótesis nula H_0. Sin embargo, ¿qué tan lejos de 0 es suficiente? Para responder esta pregunta estimamos la estadística t:
La ecuación anterior significa “cuántas desviaciones estándar se encuentra b_1 alejado del 0”. Si no hubiera relación entre X y Y, esperaríamos que t siguiera una distribución t con n-2 grados de libertad. Por lo tanto, podemos calcular el valor p y, si este valor es lo suficientemente chico (tradicionalmente menor a 0.05 o 0.01 es suficiente dependiendo que tanta precisión querramos), podemos rechazar H_0. El valor p básicamente nos dice cual es la probabilidad de que la relación observada sea casualidad (i.e. si el valor p es 0.01, quiere decir que existe 1% de probabilidad de que la relación sea casualidad). En nuestro caso vemos lo siguiente:
Entonces concluímos que sí existe una relación entre las ventas y el gasto en publicidad en televisión (por que el valor p de TV, que es la última columna de la tabla anterior, es menor a 0.01).
2.3 Precisión del modelo
Una vez que determinamos que efectivamente hay una relación entre X y Y, lo siguiente que queremos hacer es cuantificar que tan bien se ajusta el modelo a los datos. Para esto a mi me gusta utilizar la medida R^2 (aunque existen otras más). Para calcularla usamos la siguiente ecuación:
donde
TSS mide la varianza total de Y y RSS mide la varianza que queda “sin explicación” después de la regresion. Por lo tanto, R^2 nos dice la proporción de variabilidad en Y que puede ser explicada usando X. En nuestro caso, R^2=0.8122, o sea que el gasto en TV explica el 81.22% de la variabilidad en ventas.
3 Regresión lineal múltiple
Cuando estamos hablando de un descriptor y una respuesta, podemos imaginarnos el problema como intentar trazar una línea a través de los puntos. Cuando tenemos dos descriptores y una respuesta, podemos pensar en un plano en espacio tridimensional. Sin embargo, de tres descriptores en adelante es difícil poder visualizarlo. Vamos a tener que depender de los números.
3.1 Estimación de coeficientes
Antes de correr una regresión con los tres canales al mismo tiempo, veamos los coeficientes si corremos cada uno de ellos individualmente:
Por sí solos, la publicidad en televisión y radio parece tener efecto sobre las ventas. El periódico pudiera ser significativo dependiendo del nivel de confianza que utilicemos. Al 5% es significativo pero al 1% ya no lo sería. Veamos que pasa si usamos los 3 al mismo tiempo, es decir:
ventas ≅ b_0 + b_1*TV + b_2*Radio + b_3*PeriódicoEl objetivo es el mismo que en la correlación simple: encontrar la combinación b_0, b_1, b_2 y b_3 que minimicen la RSS. TV y Radio siguen siendo significativos. Pero ahora, el Periódico definitivamente ya no lo es y por mucho. ¿Tiene sentido que una variable sea significativa al considerarla por sí sola pero que al considerarla en conjunto con otra deje de serlo? La respuesta corta es: sí. La respuesta larga está escondida en la correlación de las variables que estamos utilizando:
Podemos ver que la correlación entre el gasto en radio y periódico tiene una correlación de 0.3541. Esto quiere decir que existe una tendencia a gastar más en periódico en los mercados en los que se gasta más en radio. En la correlación simple con el periódico veíamos una relación entre el gasto en periódico y las ventas, pero esto es sólo por que también estabamos gastando en publicidad en radio en estos mismos lugares. El periódico se estaba llevando el crédito por el efecto del radio sobre las ventas.
3.2 Algunas notas importantes
3.2.1 ¿Existe relación entre la respuesta y los predictores?
Esta pregunta podemos contestarla con la estadística F, que se calcula de la siguiente manera:
donde p: número de predictoresLa estadística F es análoga a la estadística t para la regresión simple. Nos ayuda a hacer la siguiente prueba de hipótesis:
H_0: b_1 = b_2 = ... = b_p = 0
H_a: por lo menos un coeficiente b_j ≠ 0Cuando H_0 es cierta, la estadística F sigue una distribución F. Y, de manera similar, podemos calcular el valor p de esta estadística para poder decidir si rechazamos o aceptamos H_0. En el caso de nuestra regresión, el valor p es muy chico y, por lo tanto, rechazamos H_0:
3.2.2 ¿Todos los predictores afectan la respuesta, o sólo algunos?
Esta tarea de determinar qué predictores son de verdad relevantes para la respuesta se conoce como selección de variables. Existen tres maneras clásicas de hacer esto con la regresión lineal:
Selección hacia adelante: Empezando con un modelo nulo, hacemos
pregresiones individuales y agregamos al modelo la que resulte en un menor RSS. Después agregamos la variable que resulte en un menor RSS para un modelo de dos predictores. Seguimos hasta que alguna regla arbitraria se cumpla (e.g. cuando alcanzamos un nivel determinado paraR^2).Selección hacia atrás: Empezamos con un modelo con todos los predictores y removemos la variable con el mayor valor p (la menos significativa). Corremos el modelo con los
p-1predictores que sobren y quitamos la siguiente variable con el mayor valor p. Seguimos hasta que alguna regla arbitraria se cumpla (e.g. cuando todas las variables que queden sean significativas).Selección mixta: Empezamos con un modelo nulo y, similar a la selección hacia adelante, vamos agregando un predictor a la vez. Si en algun punto un predictor tiene un valor p alto, lo sacamos del modelo. Continuamos estos pasos hacia adelante y hacia atrás hasta que todas las variables del modelo tengan un valor p suficientemente bajo y todas las variables descartadas tendrían un valor p alto si lo agregamos al modelo.
3.2.3 ¿Qué tan bien se ajusta el modelo a los datos?
Esto lo respondemos con la R^2 del modelo. Cuando usamos sólo TV teníamos una R^2 decente:
Al agregar Radio, tuvimos un incremento importante:
Pero, al agregar Newspaper, no hubo un incremento importante:
Esto nos da más evidencia de que Newspaper no es una variable que afecte las ventas.
3.2.4 ¿Cómo podemos predecir valores de la respuesta y qué tan buenas son estas predicciones?
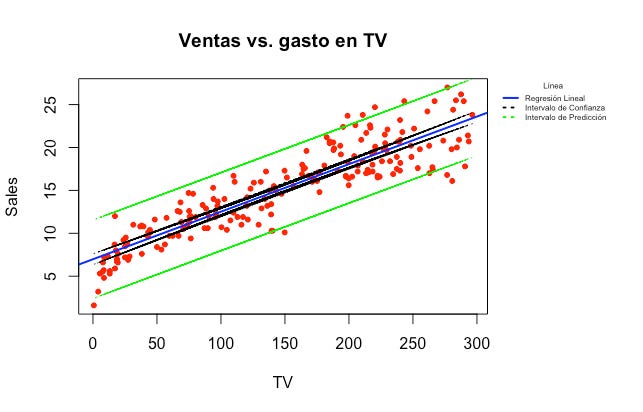
Nuestras predicciones nunca van a ser 100% atinadas desde que existe el término de error ϵ. Sin embargo, esta respuesta tiene dos caras. Lo primero que tenemos que hacer es calcular el intervalo de confianza de nuestro modelo y después el intervalo de predicción, que son dos cosas muy diferentes. Veamos a continuación con el modelo de regresión lineal simple:
El intervalo de confianza representa la incertidumbre de muestreo. Dentro de él caen el 95% de los posibles modelos que podrían haberse formado dependiendo de la muestra elegida del total de observaciones (por eso está tan cerca de la línea azul). El intervalo de predicción representa la incertidumbre de cualquier dato en particular, aparte de la incertidumbre de muestreo. Dentro de él caen el 95% de los posibles valores de la respuesta Y y por eso es mayor que el intervalo de confianza. Cuando hagamos una predicción, hay que tener esto en cuenta e incluir el intervalo que corresponda en nuestras predicciones.
4 Otras consideraciones del modelo
4.1 Predictores cualitativos
Hasta ahora hemos usado predictores puramente cuantitativos. Sin embargo, pudiera darse el caso en el que necesitemos usar predictores cualitativos (género, estado civil, etnicidad, etc). En estos casos, necesitamos crear variables dummy.
4.1.1 Predictores cualitativos con dos niveles
Predictores de este caso pueden ser el género (hombre o mujer) o su situación laboral (empleado o desempleado). Por ejemplo, imaginemos que queremos predecir la deuda de la tarjeta de crédito de una persona basados en su género. Puderíamos construir la siguiente variable dummy:
En este caso, nuestra ecuación tendría la siguiente forma:
Por lo tanto, b_0 representaría el promedio de deuda en la tarjeta de crédito para los hombres y b_1 sería la diferencia promedio entre la deuda de las mujeres y la de los hombres.
Alternativamente, pudieramos haber formado nuestra variable dummy de la siguiente manera:
En este caso, nuestra ecuación tendría la siguiente forma:
En este caso, b_0 representaría el promedio de la deuda de todas las personas, independientemente de su género. b_1 sería la cantidad por la que las mujeres están sobre el promedio y los hombres están por debajo del promedio (la mitad del b_1 estimado en el caso anterior).
Las conclusiones del modelo serían las mismas independientemente de cómo estructuremos nuestra variable dummy, pero la interpretación sería diferente.
4.1.2 Predictores cualitativos con más de dos niveles
Imaginemos ahora que queremos predecir la deuda de una persona dada su estado civil en un grupo donde hay solteros, casados y divorciados. En esta situación pudiéramos crear 2 variables dummy:
O sea que nuestra ecuación sería la siguiente:
Y los coeficientes tendrían la siguiente interpretación: b_0 es el promedio de deuda de las personas divorciadas, b_1 es la cantidad de deuda extra que tienen los casados sobre los divorciados y b_2 es la cantidad de deuda extra que tienen los solteros sobre los divorciados.
4.2 Extensiones del modelo lineal
El modelo de regresión lineal es fácil de interpretar y funciona bien en la mayoría de los casos reales. Sin embargo, tiene muchas supocisiones restrictivas que son violadas comúnmente en la práctica. Dos de estas son la suposición de que la relación entre los predictores y la respuesta es aditiva (o sea que el efecto de cambios en el precitor X_j y la respuesta Y es independiente del valor de los otros p-1 predictores) y lineal (o sea que el cambio en la respuesta Y debido al aumento unitario del predictor X_j es constante, independientemente del valor de X_j). A continuación vamos a ver qué hacer para relajar estas suposiciones.
4.2.1 Deshaciéndonos de la suposición aditiva
Anteriormente concluimos que las ventas dependían de la inversión en publicidad en televisión y radio, y que la inversión en publicidad en periódico no era relevante. Por lo tanto, hasta ahora nuestra ecuación es la siguiente y teníamos un R^2 bueno:
ventas ≅ b_0 + b_1*TV + b_2*Radio + ϵSin embargo, veamos qué pasa si incluimos un término de interacción entre estos dos predictores, de manera que nuestra ecuación sea esta:
ventas ≅ b_0 + b_1*TV + b_2*Radio + b_3*TV*Radio + ϵ
≅ b_0 + (b_1 + b_3*Radio)*TV + b_2*Radio + ϵY podemos interpretar b_3 como el incremento en la efectividad de la publicidad en TV por cada unidad de aumento en Radio.
Vemos que el efecto es estadísticamente significativo y hay un aumento en R^2:
Esto quiere decir que incluir el término de interacción entre TV y Radio ayuda a explicar (0.9127-0.9016)/(1-0.9016)=11.28% de la variabilidad en ventas que seguía sin explicación con el modelo aditivo. Siempre que incluyamos un término de interacción entre dos predictores, los predictores solos tienen que ser incluidos en la regresión, independientemente de su valor p.
4.2.2 Añadiendo relaciones no lineales
Hasta ahora no hemos visto, pero puede darse el caso que algún predictor tenga una relación no lineal con la respuesta Y. En ese caso, sería conveniente transformar el predictor elevándolo a alguna potencia mayor a 1 e incluir este predictor modificado en la regresión lineal. Después veremos algunos ejemplos donde hagamos esto.
4.3 Problemas potenciales
Cuando ajustamos un modelo lineal a los datos, muchos problemas pueden surgir. Veamos algunos de los más comunes y cómo resolverlos a continuación.
4.3.1 Relaciones no lineales entre los datos
Como ya vimos anteriormente, a veces pueden existir relaciones no lineales entre los descriptores y la respuesta Y. Es común en estos casos incluir transformaciones no lineales de los descriptores en la regresión (e.g. sqrt(X), log(X), X^2, etc).
4.3.2 Correlación entre los residuales
Una suposición importante de la regresión lineal es que los términos de error ϵ_i no tienen correlación entre ellos. En el caso de que exista correlación entre ellos, nuestros cálculos de error estándar no son confiables y, por lo tanto, nuestros intervalos de confianza tampoco son confiables. Existen varias razones y soluciones para este caso, pero lo dejaremos para ejemplos posteriores.
4.3.3 Heterocedasticidad en los residuales
La heterocedasticidad se da cuando los términos de error ϵ_i no tienen una varianza constante. Esto lo podemos ver en la gráfica de la sección 2.1, mientras más a la derecha observemos, mayores son los términos de error. En estos casos, es común arreglarlo transformando la respuesta Y con alguna función cóncava (log(Y), sqrt(Y), etc). Esto resulta en un “achatamiento” de la variable, lo cual ayuda a reducir la heterocedasticidad en los residuales.
4.3.4 Valores atípicos
Los valores atípicos son valores de la respuesta Y que están anormalmente lejos de la predicción de nuestro modelo. Estos pueden deberse a varias cosas, incluyendo un registro incorrecto de los datos. Podemos identificar estos valores atípicos por su efecto en la R^2 de nuestro modelo (i.e. al incluir el valor atípico nuestra R^2 cambia mucho). Otra manera de determinar si un valor es atípico es calcular la estadística t de los residuales. Cualquier punto con un residual estudiantizado mayor a 3 o menor a -3 puede ser considerado un valor atípico y eliminado de la regresión.
4.3.5 Puntos de palanca
Los puntos de palanca son valores de los predictores X que están anormalmente lejos del resto de los valores observados. Igual que con los valores atípicos, estos pueden ser también resultado de un registro incorrecto de los datos. Para encontrarlos podemos calcular la estadística h:
La estadística h siempre cae entre 1/n y 1, y su promedio es de (p+1)/n, así que si algún punto tiene una h mucho mayor que (p+1)/n, podemos considerarla un punto de palanca y eliminarlo de la regresión.
4.3.6 Multicolinealidad
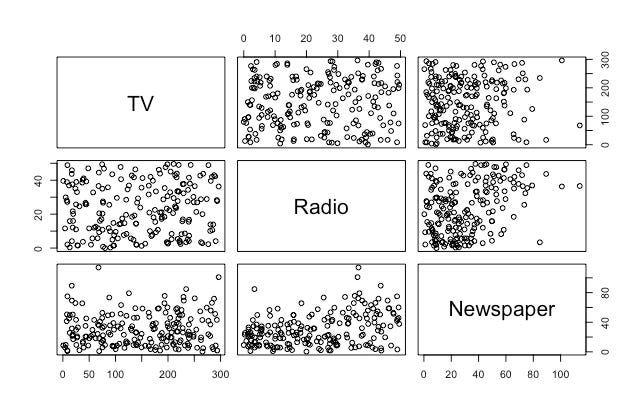
La multicolinealidad se refiere al hecho de que dos o más predictores estén relacionados entre ellos. En el caso de nuestro interés no es obvio:
Pero habrá situaciones en las que estas relaciones serán muy obvias. Si quisiéramos usar las siguientes variables como predictoras para una regresión, tendríamos un problema de multicolinealidad entre Income, Limit y Rating:
A veces esta situación es obvia a la vista (como el caso anterior), pero a veces hay que ir más allá. Otro método es revisar la matriz de correlación de las variables predictoras X. Cualquier correlación absoluta grande es indicador de un problema de multicolinealidad. Sin embargo, a veces esta situación no es evidente incluso en la matriz de correlación y hay que calcular el factor de inflación de la varianza (VIF, por sus siglas en inglés):
donde R^2_{X_j|X_-j}: la R^2 de una regresión de X_j contra
todos los otros predictoresUn valor mayor de 10 en el VIF de un predictor es considerado suficiente para determinar que existe multicolinealidad. En estos casos, hay dos soluciones simples. La primera es eliminar la(s) variable(s) problemática(s) de la regresión. La segunda es combinar las variables relacionadas en un solo predictor.
5 La respuesta a nuestras preguntas
Ahora podemos responder las preguntas originales:
¿Hay alguna relación entre el presupuesto de publicidad y las ventas? Sí, el valor p asociado a la estadística
Fes lo suficientemente bajo como para garantizar que existe una relación entre el gasto en publicidad y las ventas.Si sí, ¿qué tan fuerte es esta relación? Muy fuerte, los predictores explican el 90% de la variabilidad en las ventas.
¿Qué canales contribuyen a las ventas? Juzgando por los valores p asociados a cada variable, TV y Radio afectan las ventas pero el Periódico no.
¿Con qué grado de certeza podemos estimar el efecto de cada canal sobre las ventas? Esto se contesta con los intervalos de confianza de las variables:
¿Con qué grado de certeza podemos predecir ventas en el futuro? Dependiendo si nos referimos al intervalo de confianza o de predicción, la respuesta a esta pregunta se encuentra en ese cálculo.
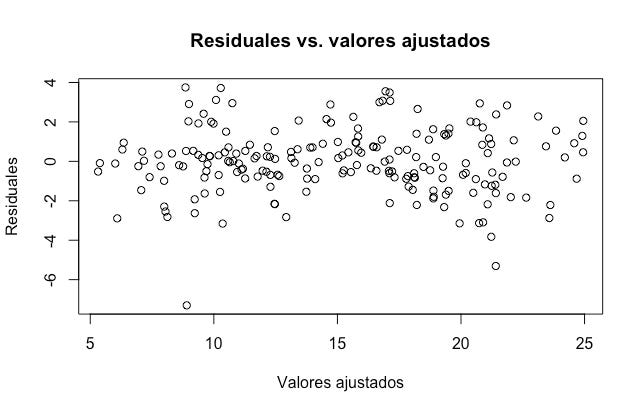
La relación entre el presupuesto de publicidad y las ventas, ¿es lineal? La gráfica de los residuales no revela ningún efecto no lineal:
¿Existen sinergias entre los diferentes canales de publicidad? Al incluir la interacción entre TV y Radio, vimos un aumento de
R^2y que la interacción era estadísticamente significativa. Concluimos que sí existen sinergias entre estos canales.
6 Regresión lineal en R
Acabo de descubrir una nueva herramienta: Google Colab. Voy a hacer las partes prácticas de estos tutoriales en esta nueva herramienta y compartirles las ligas a los cuadernos para que ustedes las puedan copiar a su propio Google Drive y modificarlas como ustedes prefieran:
Eso fue todo por hoy. Si tienen cualquier duda o comentario pueden dejarlo en la sección de abajo. Si quieren compartir este blog con sus amigos y compañeros o suscribirse, les dejo los botones aquí:
Hasta el próximo tutorial!