Opciones en R: Parte 4

El modelo binomial

Intro

En este tutorial vamos a cubrir lo siguiente:

• El modelo binomial

1 El modelo binomial

Junto con el modelo de Black-Scholes, que ya cubrimos anteriormente, el modelo binomial es el modelo más usado para calcular el precio de una opción. Este modelo tiene muchas ventajas sobre el Black-Scholes: es más simple de entender, más fácil de programar, y más flexible. Con este modelo podemos calcular precios de opciones put americanas, por ejemplo, cosa que no podíamos con el modelo Black-Scholes.

1.1 El modelo binomial para dos fechas

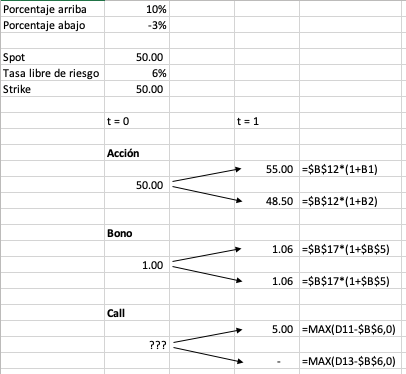
Imaginemos el siguiente ejemplo:

• Existe un periodo de tiempo con dos fechas: t=0 hoy y t=1 dentro de un año

• Existen dos activos “fundamentales”: una acción (A) y un bono (B)

• Existe un instrumento derivado: una opción call (C)sobre la acción

• El precio de la acción hoy es de $50, y dentro de un año habrá subido 10% o habrá caído -3%

• La tasa libre de riesgo para un año es de 6%

• La opción call madura en un año y el strike de la opción es $50

El reto es encontrar el precio justo del call. Veamos como a continuación:

Usemos el concepto de pricing por arbitraje, es decir, si dos o más activos tienen la misma utilidad esperada, entonces deben valer lo mismo. Encontremos una cantidad de bonos y de acciones que harían que la utilidad en ambos escenarios fuera la misma que la del call. Para eso vamos a tener que resolver el siguiente sistema de ecuaciones:

55.00*A + 1.06*B = 5
48.50*A + 1.06*B = 0

Vemos entonces que:

A = 5/(55.00 - 48.50) = 0.7692
B = (0 - 48.5*0.7692)/1.06 = -35.1959

Entonces el call debe valer:

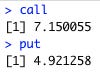
C = 0.7692*50.00 - 35.1959 = 3.2656

De igual manera podemos calcular el precio de un put:

Quise usar Excel en estos ejemplos para hacer el proceso más visual, pero veamos ahora cómo se haría en R:

# 0. Limpiar la sesión
rm(list=ls())
if (names(dev.cur()) != "null device") {
  dev.off()
}
cat("\014")

# 1. Definir el problema
p_arriba <- 0.1
p_abajo <- -0.03

spot <- 50
rf <- 0.06
strike <- 50

accion <- c(spot*(1 + p_arriba), spot*(1 + p_abajo))
bono <- rep(1 + rf, 2)

call <- pmax(accion - strike, rep(0, 2))
put <- pmax(strike - accion, rep(0, 2))

# 2. Resolver el sistema de ecuaciones y encontrar los precios
m <- matrix(c(accion, bono), nrow = 2, ncol = 2)

precio_call <- sum(solve(m, call)*c(spot, 1))
precio_put <- sum(solve(m, put)*c(spot, 1))

Y podemos ver que encontramos los mismos valores que en Excel. Nota cómo aquí no despejamos nosotros mismos como en Excel, sino que pasamos el sistema de ecuaciones a la función solve() y así encontramos los parámetros A y B.

1.1.1 Los precios de estados

Existe una manera más fácil de resolver este problema: usando state prices (o precios de estado). El razonamiento es como sigue:

Visto desde t=0 hay solo dos opciones para t=1: o sube el precio por p_arriba o cae por p_abajo. Podemos determinar un precio q_arriba de $1 en el estado “arriba” y un precio q_abajo de $1 en el estado “abajo”. Entonces el precio del bono y la acción pueden ser determinados usando estos precios:

q_arriba*spot*(1+p_arriba) + q_abajo*spot*(1+p_abajo) = spot
∴ q_arriba*(1+p_arriba) + q_abajo*(1+p_abajo) = 1

q_arriba*(1+rf) + q_abajo*(1+rf) = 1

Estas ecuaciones tienen la siguiente solución:

q_arriba = (rf - p_abajo)/[(1 + rf)*(p_arriba - p_abajo)]
q_abajo = (p_arriba - rf)/[(1 + rf)*(p_arriba - p_abajo)]

Si la acción se puede mover hacia arriba por un factor (1 + p_arriba) y hacia abajo por un factor (1 + p_abajo), y si rf es la tasa libre de riesgo del periodo, entonces el precio de cualquier otro activo puere ser calculando descontando sus pagos en el estado arriba y abajo por q_arriba y q_abajo, respectivamente. Podemos comprobar esto rápidamente en R con el mismo ejemplo de la sección anterior:

# 0. Limpiar la sesión
rm(list=ls())
if (names(dev.cur()) != "null device") {
  dev.off()
}
cat("\014")

# 1. Definir problema
p_arriba <- 0.1
p_abajo <- -0.03

spot <- 50
rf <- 0.06
strike <- 50

accion <- c(spot*(1 + p_arriba), spot*(1 + p_abajo))
bono <- rep(1 + rf, 2)

call <- pmax(accion - strike, rep(0, 2))
put <- pmax(strike - accion, rep(0, 2))

# 2. Encontrar el valor de las opciones con los
# precios de estado

q_arriba <- (rf - p_abajo)/((1 + rf)*(p_arriba - p_abajo))
q_abajo <- (p_arriba - rf)/((1 + rf)*(p_arriba - p_abajo))

precio_call <- sum(c(q_arriba, q_abajo)*call)
precio_put <- sum(c(q_arriba, q_abajo)*put)

Y vemos que, efectivamente, ambos procedimientos dan el mismo resultado.

1.2 El modelo binomial para múltiples fechas

Este modelo puede extenderse fácilmente a más de un periodo. Veamos ahora un ejemplo para dos periodos con las siguientes características:

• En cada periodo, la acción puede subir 10% o bajar -3% de su nivel en el periodo anterior

• En cada periodo, la tasa libre de riesgo es 6%

• El call madura en t=2

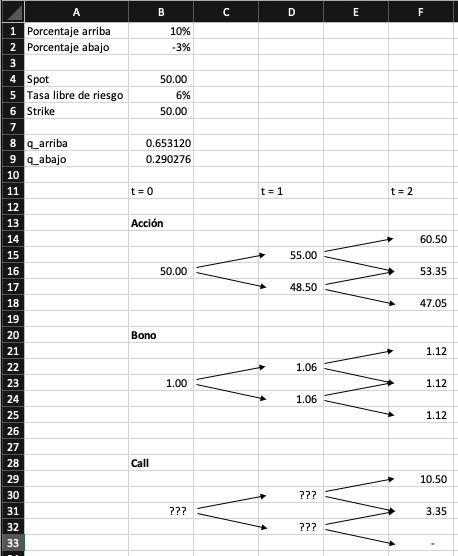
Y nuestra látice binomial se ve de la siguiente manera:

¿Cómo podemos llegar al precio del call en t=0? Hay que valuarlo hacia atrás.

En la fecha t=2 hay 3 posibles precios para la acción: $60.50 después de dos movimientos hacia arriba, $53.35 después de un movimiento hacia arriba y uno hacia abajo (o uno hacia abajo y luego uno hacia arriba, es lo mismo), o $47.05 después de dos mocimientos hacia abajo. Dados estos precios, el call en t=2 valdrá $10.50, $3.35 o $0, respectivamente.

En la fecha t=1 hay dos posibilidades. Analicemos primero el estado arriba, donde la acción vale $55 y la opción valdrá $10.50 o $3.35 a expiración:

Podemos usar los parámetros q_arriba y q_abajo para encontrar el precio de la opción en este escenario

C(celda D30) = q_arriba*10.50 + q_abajo*3.35 = 7.83

De manera similar para el estado abajo:

C(celda D32) = q_arriba*3.35 + q_abajo*0.00 = 2.19

Siguiendo esta misma lógica, para t=0 el precio del call estará dado por:

C(celda B31) = q_arriba*7.83 + q_abajo*2.19 = 5.75

Y nuestra látice binomial está completa:

Este mismo proceso se puede extender a muchos periodos y llegamos a la conclusión que los precios de un call y un put europeo según esta látice binomial para n periodos están dados por:

donde n: número de periodos
      S: precio spot de la acción
      U: (1 + p_arriba)
      D: (1 + p_abajo)
      K: strike de la opción

De nuevo, estas fórmulas podemos usarlas para opciones europeas. En el caso de opciones americanas, habrá que hacer todo el proceso que hicimos anteriormente, calculando su valor hacia atrás.

Implementemos estas dos ecuaciones en R (recuerden agregar esto a su archivo herramientas.R):

binom <- function(n, i) {
  
  # Calcula el coeficiente binomial (n i) = n!/(i!(n - i)!)
  # Se necesita:
  # - n
  # - i
  # Se regresa:
  # El coeficiente binomial (n i) "n choose i"
  
  return(factorial(n)/(factorial(i)*factorial(n - i)))
}

binom.eur.model <- function(p_arriba, p_abajo, rf, spot,
                        strike, periodos, tipo = "c") {
  
  # Calcula el precio teórico de una opción europea usando el
  # modelo binomial (1979)
  # Se necesita:
  # - p_arriba: movimiento hacia arriba (porcentaje en decimal)
  # - p_abajo: movimiento hacia abajo (porcentaje en decimal)
  # - rf: tasa libre de riesgo del periodo
  # - spot: precio spot del subyacente al momento de valuación
  # - strike: strike de la opción
  # - periodos: numero de pasos en la látice binomial
  # - tipo: "c" (call) o "p" (put)
  # Se regresa:
  # El precio de la opción según el modelo binomial (1979)
  
  tipo = tolower(tipo)
  
  if (!(tipo %in% c("c", "p"))) {
    stop("El tipo de la opción es incorrecto.
         Elige uno de 'c' (call) o 'p' (put).")
  }
  
  q_arriba <- (rf - p_abajo)/((1 + rf)*(p_arriba - p_abajo))
  q_abajo <- (p_arriba - rf)/((1 + rf)*(p_arriba - p_abajo))
  
  i <- seq(0, periodos, by = 1)
  value <- 0
  
  for (paso in i) {
    if (tipo == "c") {
      value <- value + binom(periodos, paso)*q_arriba^paso*
        q_abajo^(periodos - paso)*
        max(spot*(1 + p_arriba)^paso*
              (1 + p_abajo)^(periodos - paso) - strike, 0)
    } else {
      value <- value + binom(periodos, paso)*q_arriba^paso*
        q_abajo^(periodos - paso)*
        max(strike - spot*(1 + p_arriba)^paso*
              (1 + p_abajo)^(periodos - paso), 0)
    }
  }
  
  return(value)
}

La función binom() genera el coeficiente binomial requerido para la fórmula. No hay una función nativa de R que nos proporcione este valor, así que nosotros creamos una propia. El for de la función binom.eur.model() se puede evitar si hacemos uso de funciones nativas de R y así podemos hacer más rápida esta función. Les dejo como ejercicio hacer esta modificación (pista: son funciones que ya hemos usado en este mismo tutorial).

1.3 ¿Cómo elegir p_arriba y p_abajo?

La elección de los parámetros p_arriba y p_abajo va a depender de las características de riesgo y retorno de la acción. En tutoriales anteriores les enseñé cómo calcular el retorno promedio (𝜇) y la volatilidad (𝞼) de una acción. También depende del número de periodos que utilicemos. Veamos el siguiente caso:

• La acción tiene retorno promedio 𝜇 = 15% y volatilidad 𝞼 = 35%

• La tasa libre de riesgo es de 6%

• El precio de la acción en este momento es $50

• Queremos encontrar el precio de las opciones europeas call y put con strike de $50 y vencimiento en 9 meses (0.75 años)

• Vamos a dividir el año en 25 intervalos iguales (cada división ∆t=1/25=0.04) y, por lo tanto, nuestra látice tiene 19 periodos (0.75*25 = 18.75 y redondeamos a 19 porque no puede haber periodos fraccionales)

Entonces p_arriba y p_abajo están dados por:

p_arriba = exp(𝜇*∆t + 𝜎*sqrt(∆t)) - 1
p_abajo = exp(𝜇*∆t - 𝜎*sqrt(∆t)) - 1

Podemos ignorar el 𝜇*∆t, pero yo prefiero incluirlo.

El precio entonces de la opción se calcula de la siguiente manera:

# 0. Limpiar la sesión
rm(list=ls())
if (names(dev.cur()) != "null device") {
  dev.off()
}
cat("\014")

# 1. Cargar herramientas
source("scripts/herramientas.R")

# 2. Calcular precio de opciones europeas con modelo binomial
ret_promedio <- 0.15
sigma <- 0.35
rf_anual <- 0.06

spot <- 50
strike <- 50
t <- 0.75
divisiones <- 25
delta_t <- 1/divisiones
periodos <- round(t*divisiones)
p_arriba <- exp(ret_promedio*delta_t + sigma*sqrt(delta_t)) - 1
p_abajo <- exp(ret_promedio*delta_t - sigma*sqrt(delta_t)) - 1
rf <- exp(rf_anual*delta_t) - 1

call <- binom.eur.model(p_arriba, p_abajo, rf,
                    spot, strike, periodos)
put <- binom.eur.model(p_arriba, p_abajo, rf,
                   spot, strike, periodos, "p")

1.4 Convergencia del modelo binomial y el modelo Black-Scholes para opciones europeas

En el caso de opciones europeas, para el cual el modelo Black-Scholes es muy útil, podemos ver que el modelo binomial no da los mismos resultados. Usando los parámetros de la sección anterior vemos que el precio para las mismas opciones según el modelo Black-Scholes no es el mismo:

call_bs <- black.scholes.model(strike, spot, rf_anual,
                               t, sigma)
put_bs <- black.scholes.model(strike, spot, rf_anual,
                              t, sigma, "p")

Sin embargo, conforme aumentamos el numero de divisiones del año, lo que equivale a aumentar el número de periodos en la látice, vemos como ambos modelos convergen a la misma respuesta. Agregamos lo siguiente al script de la sección anterior:

# 3. Convergencia del modelo binomial y Black-Scholes
calls <- c()
puts <- c()

divisiones <- seq(10, 200, by = 10)

for (division in divisiones) {
  delta_t <- 1/division
  periodos <- round(t*division)
  p_arriba <- exp(ret_promedio*delta_t +
                    sigma*sqrt(delta_t))- 1
  p_abajo <- exp(ret_promedio*delta_t -
                   sigma*sqrt(delta_t)) - 1
  rf <- exp(rf_anual*delta_t) - 1

  call <- binom.eur.model(p_arriba, p_abajo, rf,
                      spot, strike, periodos)
  put <- binom.eur.model(p_arriba, p_abajo, rf,
                     spot, strike, periodos, "p")

  calls <- c(calls, call)
  puts <- c(puts, put)
}

call_bs <- black.scholes.model(strike, spot, rf_anual,
                               t, sigma)
put_bs <- black.scholes.model(strike, spot, rf_anual,
                              t, sigma, "p")

plot(divisiones, calls, type = "l", lwd = 2,
     main = "Convergencia del call binomial y Black-Scholes",
     ylab = "Valor del call ($)", xlab = "Divisiones de t")
abline(h = call_bs, col = "red", lwd = 2)
legend("topright", lty = 1, col = c("black", "red"), lwd = 2,
       legend = c("Binomial", "Black-Scholes"), box.lty = 0,
       title = "Modelo", inset = c(0.05, 0.05))

plot(divisiones, puts, type = "l", lwd = 2,
     main = "Convergencia del put binomial y Black-Scholes",
     ylab = "Valor del put ($)", xlab = "Divisiones de t")
abline(h = put_bs, col = "red", lwd = 2)
legend("topright", lty = 1, col = c("black", "red"), lwd = 2,
       legend = c("Binomial", "Black-Scholes"), box.lty = 0,
       title = "Modelo", inset = c(0.05, 0.05))

Eso fue todo por hoy. Espero que este tutorial les haya servido. En el próximo tutorial vamos a ver como usar este modelo para calcular precios de opciones americanas, y más cosas interesantes. Si tienen cualquier duda o comentario pueden dejarlo en la sección de abajo. Si quieren compartir este blog con sus amigos y compañeros o suscribirse, les dejo los botones aquí:

Hasta el próximo tutorial!