Optimización de portafolios en R: Parte 1

Introducción

Intro

En este tutorial vamos a cubrir lo siguiente:

• Introducción a la optimización de portafolios

• Optimización de portafolios con tseries

1. Introducción a la optimización de portafolios

Anteriormente vimos cómo crear un portafolio con pesos arbitrarios para nuestros activos en formato buy and hold y con rebalanceos periódicos. La optimización de portafolios nos permite contestar a la pregunta: ¿qué peso debería tener cada activo en mi portafolio? Dependiendo del objetivo que queramos lograr (maximizar la proporción de retorno esperado y varianza, minimizar el riesgo del portafolio, etc.), los procedimientos de optimización que veremos a continuación nos permitirán encontrar los pesos de cada acción o ETF en nuestro portafolio para lograrlo.

2. Optimización de portafolios con tseries

La librería tseries es una colección de funciones para análisis de series de tiempo y finanzas computacionales disponible en R. Usaremos varias funciones de este paquete para resolver problemas básicos de optimización de portafolios.

2.1 Calculando R y 𝝨

Antes de empezar a optimizar un portafolio necesitamos dos elementos, según vimos en el tutorial anterior, el vector de retornos esperados y la matriz de covarianza:

# 0. Limpiar la sesión
rm(list=ls())
if (names(dev.cur()) != "null device") {
  dev.off()
}
cat("\014")

# 1. Cargar librerías
library(quantmod)
library(tseries)
library(PerformanceAnalytics)
library(ggplot2)
library(reshape2)

# 2. Descargar datos y extraer precios ajustados
etf_data <- new.env()
etfs <- c("VOX", "VCR", "VDC", "VDE", "VFH", "VHT", "VIS", "VGT", "VAW", "VNQ", "VPU")
getSymbols(etfs, env = etf_data, from = "2011-11-19")
adj_list <- lapply(etf_data, Ad)
adj_ts <- do.call(merge, adj_list)
names(adj_ts) <- gsub(".Adjusted", "", names(adj_ts))

# 3. Calcular retornos
adj_rets <- na.omit(Return.calculate(adj_ts))

# 4. Calcular vector de retornos esperados y matriz de covarianza (anualizados)
R <- Return.annualized(adj_rets)
Sigma <- cov(adj_rets)*252
sigma <- StdDev.annualized(adj_rets)

# 5. Graficar el espectro riesgo-retorno de los activos en mi universo de inversión
plot(sigma, R, 
     main= "Espectro riesgo-retorno para los 11 ETFs",
     xlab= "Riesgo",
     ylab= "Retorno",
     col= "blue", pch = 19, cex = 1, lty = "solid", lwd = 2,
     xlim = c(.13 , .29)) 
text(sigma, R, labels = names(adj_rets), cex= 0.7, pos = 4)

Vamos a usar los 11 ETFs de sectores que Vanguard tiene disponibles para nuestro análisis. El script anterior simplemente baja los datos y calcula el vector R y la matriz 𝝨 como ya hemos hecho anteriormente y nos muestra la posición de cada uno de los activos en nuestro universo de inversión en el espectro riesgo-retorno.

2.2 El portafolio óptimo con el retorno promedio

El paquete tseries tiene la función portfolio.optim( ), la cual nos permite llevar a cabo la optimización de nuestro portafolio. Por default, esta función calcula el portafolio óptimo para el retorno promedio de nuestra muestra (es decir, el retorno del portafolio con mismos pesos para todos los activos: e.g. 1/11 = 9.09% a cada activo). Veamos como funciona esto:

# 6. Portafolio óptimo con tseries
opt <- portfolio.optim(adj_rets)
mismos_pesos <- rep(1/ncol(adj_rets), ncol(adj_rets))
opt_pesos <- opt$pw
mismos_pesos_stdev <- sqrt(mismos_pesos %*% Sigma %*% t(t(mismos_pesos)))
opt_pesos_stdev <- sqrt(opt_pesos %*% Sigma %*% t(t(opt_pesos)))

# 7. Comparación de pesos óptimos vs. mismos pesos
pesos_df <- data.frame(names(adj_rets), mismos_pesos, opt_pesos)
pesos_mdf <- melt(pesos_df, id.vars = "names.adj_rets.")
p <- ggplot(pesos_mdf, aes(x=names.adj_rets., y=value, fill=variable)) +
  labs(x = "ETFs", y = "Peso en el portafolio",
       title = "Comparación de pesos (Mismos pesos vs. Optimizado)") +
  scale_fill_discrete(name = "Portafolio",
                      breaks = c("mismos_pesos", "opt_pesos"),
                      labels = c("Mismos pesos", "Optimizado")) +
  geom_bar(stat='identity', position='dodge')
print(p)

Podemos ver que tseries encontró un portafolio con el mismo retorno que el portafolio con mismos pesos que podemos construir con sólo 4 activos: 57% en VDC, 18% en VCR, 18% en VHT y 7% en VPU. Este portafolio tiene una volatilidad de 13.7% vs. 16.2% para el portafolio de mismos pesos. Teóricamente, no habría razón para que un inversionista escogiera el portafolio de mismos pesos cuando existe este portafolio óptimo que da el mismo retorno esperado pero con una volatilidad menor.

2.3 Construyendo la frontera eficiente

Para poder calcular la frontera eficiente con tseries, necesitamos pasarle a la función portfolio.optim( ) diferentes puntos de retorno objetivo para que calcule los pesos del portafolio óptimo en ese punto. Una vez que tenemos estos pesos, podemos calcular el retorno esperado y la volatilidad de ese portafolio. La colección de todos estos portafolios irán formando nuestra frontera eficiente:

# 8. Calculando la frontera eficiente con tseries
puntos_fe <- 100
mu <- colMeans(adj_rets)
mus <- seq(from = min(mu) + 1e-6, to = max(mu) - 1e-6, length.out = puntos_fe)
mu_fe <- sigma_fe <- rep(NA, puntos_fe)
pesos_fe <- matrix(NA, puntos_fe, ncol(adj_rets))

for(i in 1:length(mus)) {
  opt <- portfolio.optim(x = adj_rets, pm = mus[i])
  mu_fe[i] <- opt$pw %*% t(R)
  sigma_fe[i] <- sqrt(t(opt$pw) %*% Sigma %*% opt$pw)
  pesos_fe[i, ] <- opt$pw
}

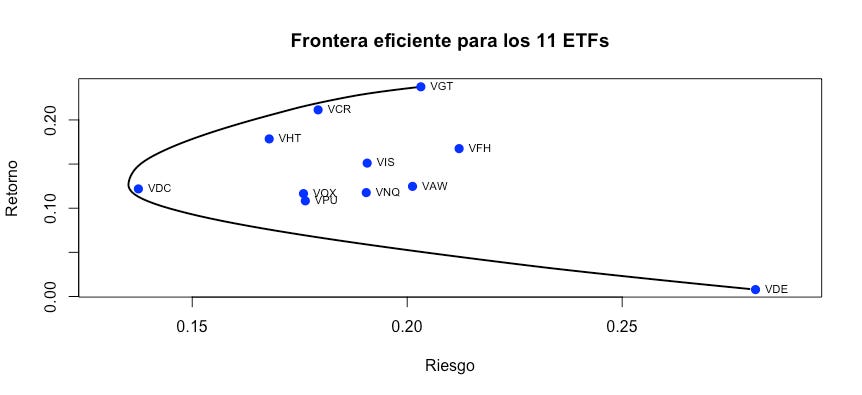
plot(sigma_fe, mu_fe, 
     main= "Frontera eficiente para los 11 ETFs",
     xlab= "Riesgo",
     ylab= "Retorno",
     type = "l", lwd = 2,
     xlim = c(.13 , .29))
points(sigma, R,
     col= "blue", pch = 19, cex = 1, lty = "solid", lwd = 2) 
text(sigma, R, labels = names(adj_rets), cex= 0.7, pos = 4)

Nota que, aunque nuestra frontera tiene un lado superior y un lado inferior, un inversionista razonable sólo estaría interesado en la parte superior de la frontera eficiente, pues le ofrece un mayor rendimiento con la misma volatilidad que los portafolios en el lado inferior.

2.3.1 El portafolio tangente y el portafolio de mínima varianza

En el tutorial anterior platicamos sobre el portafolio tangente, o el portafolio de máximo índide Sharpe (MSR por sus siglas en inglés). Este portafolio es importante porque, (de nuevo) teóricamente, es el portafolio que ofrece la mejor relación posible entre retorno y riesgo.

Otro portafolio de interés en la frontera es el extremo izquerdo (la “nariz”) de la frontera eficiente. Este portafolio se conoce como el portafolio de mínima varianza global (GMV por sus siglas en inglés).

Dado que ya hemos calculado la frontera eficiente, encontrar estos dos portafolios es relativamente fácil:

# 9. Identificando los portafolios MSR y GMV
rf_rate <- 0.02

# MSR
sharpe_ratios <- (mu_fe - rf_rate)/sigma_fe
pesos_msr <- pesos_fe[sharpe_ratios == max(sharpe_ratios), ]
mu_msr <- mu_fe[sharpe_ratios == max(sharpe_ratios)]
sigma_msr <- sigma_fe[sharpe_ratios == max(sharpe_ratios)]

# GMV
pesos_gmv <- pesos_fe[sigma_fe == min(sigma_fe), ]
mu_gmv <- mu_fe[sigma_fe == min(sigma_fe)]
sigma_gmv <- sigma_fe[sigma_fe == min(sigma_fe)]

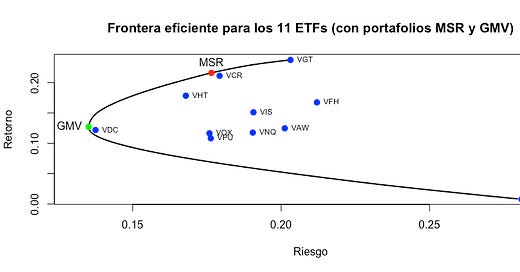
plot(sigma_fe, mu_fe, 
     main= "Frontera eficiente para los 11 ETFs (con portafolios MSR y GMV)",
     xlab= "Riesgo",
     ylab= "Retorno",
     type = "l", lwd = 2,
     xlim = c(.13 , .29))
points(sigma, R,
       col= "blue", pch = 19, cex = 1, lty = "solid", lwd = 2)
text(sigma, R, labels = names(adj_rets), cex= 0.7, pos = 4)
points(c(sigma_msr, sigma_gmv), c(mu_msr, mu_gmv),
       col= c("red", "green"), pch = 19, cex = 1, lty = "solid", lwd = 2)
text(c(sigma_msr, sigma_gmv), c(mu_msr, mu_gmv),
     labels = c("MSR", "GMV"), cex= 1, pos = c(3,2))

Y podemos comparar los pesos de cada activo en ambos portafolios de la siguiente manera:

# 10. Comparación de portafolios MSR y GMV
pesos_df <- data.frame(names(adj_rets), pesos_msr, pesos_gmv)
pesos_mdf <- melt(pesos_df, id.vars = "names.adj_rets.")
p <- ggplot(pesos_mdf, aes(x=names.adj_rets., y=value, fill=variable)) +
  labs(x = "ETFs", y = "Peso en el portafolio",
       title = "Comparación de pesos (MSR vs. GMV)") +
  scale_fill_discrete(name = "Portafolio",
                      breaks = c("pesos_msr", "pesos_gmv"),
                      labels = c("MSR", "GMV")) +
  geom_bar(stat='identity', position='dodge')
print(p)

2.4 Una advertencia en este cuento

A lo largo de los años, esta manera de construir portafolios ha sido muy estudiada. Uno de los mayores problemas con este procedimiento es que genera portafolios muy concentrados, como pueden ver en las gráficas de pesos anteriores. La mayoría de los inversionistas no se sentirían agusto invirtiendo 70% de su portafolio en VDC, como les dictaría el portafolio GMV, o teniendo más del 80% de su portafolio en 2 de 11 industrias, como les dice el portafolio MSR. El problema de la concentarción de pesos viene de un problema de estimación. La optimización de Markowitz es demasiado sensible a los parámetros iniciales que calculamos, R y 𝝨, e incluso variaciones pequeñas en estos parámetros tienden a generar resultados muy diferentes en los pesos calculados para los portafolios.

Otra crítica hacia los portafolios “a la Markowitz” es que tienden a no funcionar muy bien fuera de la muestra. Es decir, el portafolio de máximo índice Sharpe tiende a no ser la mejor inversión para el futuro puesto que fue estimado con parámetros históricos muy sensibles. Veamos ese efecto a continuación, calculando el MSR a finales del 2016 y viendo cómo se hubiera comportado estos últimos 5 años vs. otros esquemas de inversión:

# 11. Rendimiento del MSR vs mismos pesos a partir del 2017
train_rets <- adj_rets["/2016"]
test_rets <- adj_rets["2017/"]

train_R <- Return.annualized(train_rets)
train_Sigma <- cov(train_rets)*252

puntos_fe <- 100
mu <- colMeans(train_rets)
mus <- seq(from = min(mu) + 1e-6, to = max(mu) - 1e-6, length.out = puntos_fe)
mu_fe <- sigma_fe <- rep(NA, puntos_fe)
pesos_fe <- matrix(NA, puntos_fe, ncol(adj_rets))

for(i in 1:length(mus)) {
  opt <- portfolio.optim(x = train_rets, pm = mus[i])
  mu_fe[i] <- opt$pw %*% t(train_R)
  sigma_fe[i] <- sqrt(t(opt$pw) %*% train_Sigma %*% opt$pw)
  pesos_fe[i, ] <- opt$pw
}

# MSR
rf_rate <- 0.02
sharpe_ratios <- (mu_fe - rf_rate)/sigma_fe
pesos_msr <- pesos_fe[sharpe_ratios == max(sharpe_ratios)]

# GMV
pesos_gmv <- pesos_fe[sigma_fe == min(sigma_fe), ]

test_msr_rets <- Return.portfolio(test_rets, weights = pesos_msr)
names(test_msr_rets) <- "MSR"
test_gmv_rets <- Return.portfolio(test_rets, weights = pesos_gmv)
names(test_gmv_rets) <- "GMV"
test_mismos_pesos_rets <- Return.portfolio(test_rets, weights = mismos_pesos)
names(test_mismos_pesos_rets) <- "MismosPesos"
rets <- cbind(test_msr_rets, test_gmv_rets, test_mismos_pesos_rets)

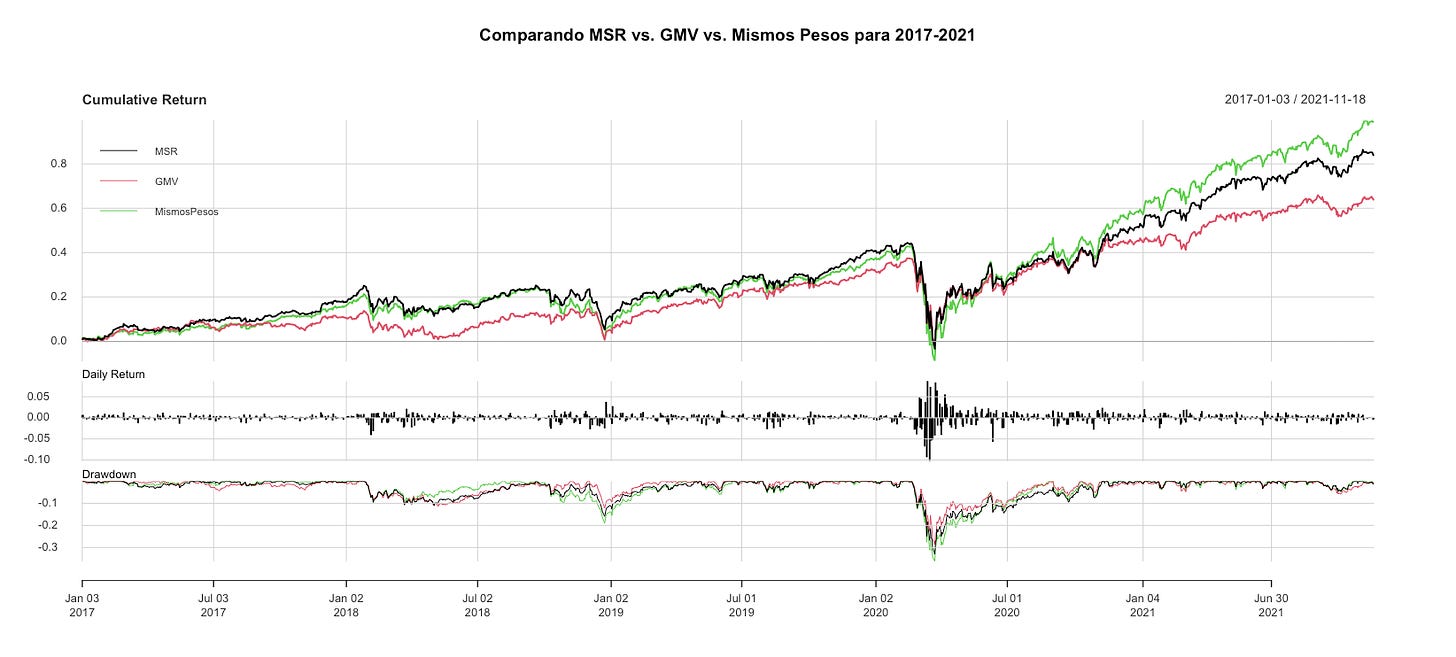
charts.PerformanceSummary(rets, main = "Comparando MSR vs. GMV vs. Mismos Pesos para 2017-2021")
print(table.AnnualizedReturns(rets))

Para este periodo de 5 años, un portafolio de mismos pesos (que no toma esfuerzo calcularlo) tuvo mejor rendimiento y mejor índice Sharpe vs. el MSR (15.13% y 0.80 anualizado vs. 13.27% y 0.75 anualizado, respectivamente).

Sin embargo, no todo está perdido. En el siguiente tutorial vamos a explorar otro paquete de R que nos permitirá hacer optimizaciones más realistas y veremos que tan eficiente es de verdad esta técnica vs. otras.

Hasta el próximo tutorial!