Análisis de portafolios en R

Intro

En este tutorial vamos a cubrir lo siguiente:

• Pesos y retornos de portafolios

• Análisis del rendimiento y riesgo de un portafolio

1. Pesos y retornos de portafolios

Cuando hablamos de portafolios de inversión, hablamos de invertir una colección de activos diferentes en una proporción determinada. Por ejemplo, en el caso de un portafolio conformado por 2 ETFs: VTI y VXUS, estos son los componentes del portafolio y los pesos están dados por la proporción en la que nuestros recursos están invertidos en estos componentes (60%/40%, 50%/50%, etc).

Los pesos de nuestro portafolio no son estáticos, cambian conforme el valor de los activos cambia. Por ejemplo, si creamos un portafolio de $1,000 USD con pesos 50%/50% en estos dos activos, estaríamos invirtiendo $500 en VTI y $500 en VXUS. Si al día siguiente VTI sube 10% y VXUS baja 20%, nuestro portafolio ahora valdría $950 USD: $550 estarían invertidos en VTI ($550/$950 = 57.89%) y $400 en VXUS ($400/$950 = 42.11%).

El retorno del portafolio está dado por los pesos iniciales multiplicados por el rendimiento aritmético de cada activo: 50% * 10% + 50% * (-20%) = -5%. El siguiente día, los pesos habrían cambiado y el rendimiento también. Suponiendo que ahora VTI cae 10% y VXUS sube 25%, el rendimiento del portafolio para este segundo día sería: 57.89% * (-10%) + 42.11% * 25% = 4.74%.

1.1 Usando PerformanceAnalytics para calcular series de tiempo de pesos y retornos

Por suerte para nosotros, PerformanceAnalytics viene con funciones que simplifican todos estos cálculos. Vamos a simular el caso en el que creamos un portafolio de 50% VTI y 50% VXUS a principios del 2021 y calcularemos con ayuda de este paquete sus retornos YTD y la evolución de los pesos de nuestro portafolio (como no vamos a rebalancear en este momento, esta estrategia la nombraremos buy and hold):

# Cargar librerías necesarias
library(quantmod)
library(PerformanceAnalytics)

# Ajustar defaults para getSymbols
setDefaults(getSymbols.yahoo, from = "2020-12-31")

# Crear ambiente para datos y bajarlos
etf_data <- new.env()
etfs <- c("VTI", "VXUS")
getSymbols(etfs, env = etf_data)

# Combinar la columna "Adjusted" de cada ETF en una sola serie de tiempo
adj_list <- lapply(etf_data, Ad)
adj_prices <- do.call(merge, adj_list)
names(adj_prices) <- gsub(".Adjusted", "", names(adj_prices))

# Limpiar la serie de tiempo omitiendo NAs
adj_prices <- na.omit(adj_prices)

# Definir pesos en el portafolio
weights <- c(0.5, 0.5)

# Calcular retornos de los ETFs y del portafolio buy-and-hold y graficarlos
adj_rets <- na.omit(Return.calculate(adj_prices))
buy_and_hold <- Return.portfolio(adj_rets, weights)
names(buy_and_hold) <- c("BuyAndHold")
all_rets <- cbind(adj_rets, buy_and_hold)
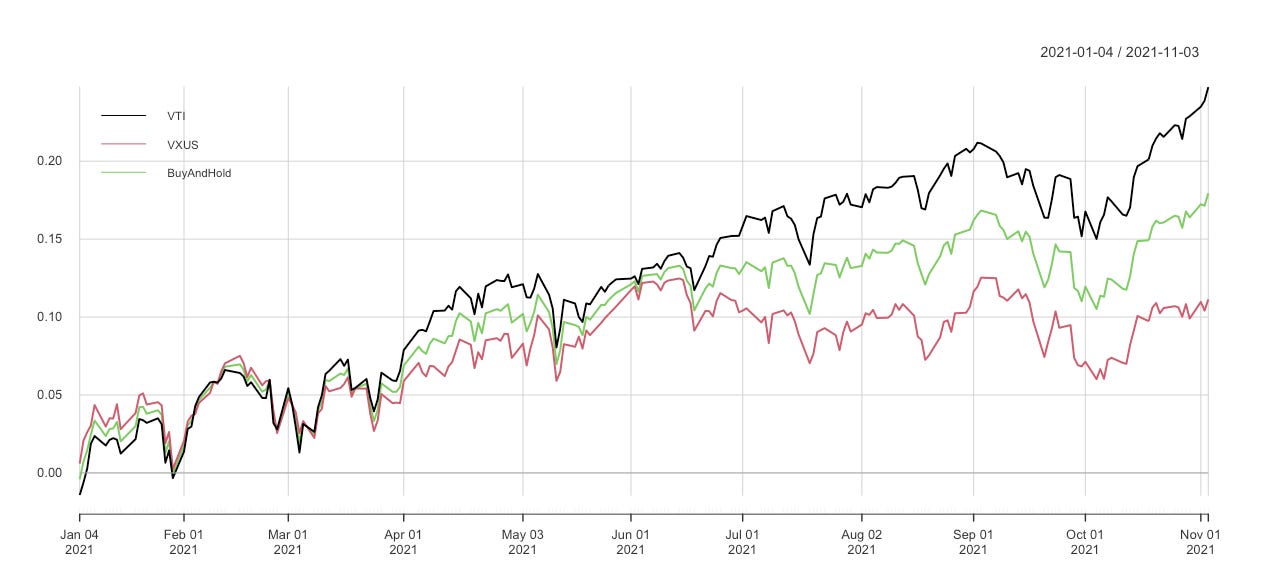
print(chart.CumReturns(all_rets, legend.loc = "topleft"))

Rendimiento YTD de la estrategia buy and hold comparada contra VTI y VXUS.

Si queremos analizar la evolución de los pesos de nuestra estrategia buy and hold, podemos usar el parametro verbose de la función Return.portfolio( ). Esto hace que la función nos regrese una lista de diferentes variables que podemos después analizar:

buy_and_hold_info <- Return.portfolio(adj_rets, weights, verbose = TRUE)
chart.TimeSeries(buy_and_hold_info$BOP.Weight, legend.loc = "topleft")

Evolución de pesos para la estrategia buy and hold.

Podemos ver como ambos activos representaban el 50% de nuestro portafolio el primer día, pero conforme fue avanzando el tiempo estos pesos fueron cambiando hasta que VTI representa el 52.87% del portafolio y VXUS el 47.13% el 3 de noviembre de 2021. Nuestra variable buy_and_hold_info contiene mucha información de nuestro portafolio: los retornos (returns), la contribución de cada activo al retorno del portafolio (contribution), el valor inicial de cada posición y su peso (BOP.Value y BOP.Weight, respectivamente) y valor final de cada posición y su peso (EOP.Value y EOP.Weight, respectivamente).

También podemos usar estas funciones para crear portafolios rebalanceados. Modifiquemos la última parte de nuestro script para incluir un portafolio rebalanceado cada mes en nuestra comparación con pesos 60% VTI y 40% VXUS (a esta estrategia la llamaremos monthly rebal.):

# Definir pesos en el portafolio
weights <- c(0.5, 0.5)

# Calcular retornos de los ETFs, del portafolio buy-and-hold, y del portafolio rebalanceado mensualmente y graficarlos
adj_rets <- na.omit(Return.calculate(adj_prices))
buy_and_hold <- Return.portfolio(adj_rets, weights)
monthly_rebal <- Return.portfolio(adj_rets, weights, rebalance_on = "months")
names(buy_and_hold) <- c("BuyAndHold.5050")
names(monthly_rebal) <- c("MonthlyRebal.5050")
all_rets <- cbind(adj_rets, buy_and_hold, monthly_rebal)
print(chart.CumReturns(all_rets, legend.loc = "topleft"))

Agregando comparación con la estrategia monthly rebal.

La estrategia no se ve en la gráfica por que el rendimiento es prácticamente el mismo que buy and hold, pero si hacen zoom en sus pantallas van a ver que está ahí. Y podemos ver que los pesos de esta estrategia se “resetean” todos los meses a 50%/50% en vez de que se muevan libremente como en buy and hold:

monthly_rebal_info <- Return.portfolio(adj_rets, weights, rebalance_on = "months", verbose = TRUE)
chart.TimeSeries(monthly_rebal_info$BOP.Weight, legend.loc = "topleft")

Evolución de pesos para la estrategia monthly rebal.

Evidentemente estos efectos son mucho más notorios si usamos dos activos que hayan tenido comportamientos muy diferentes. A continuación muestro que hubiera pasado si en vez de usar VTI y VXUS hubieramos usado GME y KO:

Comparación de estrategias buy and hold y monthly_rebal usando GME y KO.

Evolución de precios para la estrategia buy and hold.

Evolución de pesos para la estrategia monthly rebal.

2. Análisis del rendimiento y riesgo de un portafolio

Cuando hacemos análisis del rendimiento de un portafolio nos interesan 2 cosas principalmente:

• Describir el comportamiento observado anteriormente (a esto lo llamamos el análisis ex-post)

• Hacer predicciones razonables sobre su comportamiento futuro (a esto lo llamamos el análisis ex-ante)

Para los siguientes pasos, vamos a analizar el S&P 500 como si este fuera nuestro portafolio.

2.1 Rendimientos del portafolio

2.1.1 Rendimiento promedio de un portafolio

Una métrica importante al hablar de un portafolio es su rendimiento promedio. Sin embargo, hay que tomar en cuenta que los rendimientos geométricos no se compensan linealmente. Es decir, si en el día 1 mi portafolio sube 50% y en el día 2 baja 50%, no me quedé igual que en el día 0:

v_0 * (1 + 0.5) * (1 - 0.5) = 0.75 * v_0

Así que simplemente tomar el promedio de los rendimientos sería equivocado. Tenemos que tomar la media geométrica de los retornos, que está dada por:

[(1 + r_1) * (1 + r_2) * ... * (1 + r_T)] ^ (1/T) - 1

donde r_t: el rendimiento del día t de 1 a T

e.g. [(1 + 0.5) * (1 - 0.5)] ^ (1/2) - 1 = -13.4%

O sea que crecer un día a 50% y el otro caer 50% no es equivalente a crecer 0% sino a caer 13.4% cada día (usa R para comprobarlo).

Aclarado este punto, podemos usar la función mean.geometric( ) de PerformanceAnalytics para calcular este importante parámetro:

# Análisis del S&P 500 (mensual)
sp500 <- na.omit(Ad(getSymbols("^GSPC", from = "1989-12-31", auto.assign = FALSE)))
sp500_monthly_prices <- sp500[endpoints(sp500)]
sp500_monthly_rets <- Return.calculate(sp500_monthly_prices)
sp500_mean_ret <- mean.geometric(sp500_monthly_rets)

Y podemos concluir que el S&P 500 ha tenido un rendimiento promedio mensual de 0.7% de 1990 a la fecha. Usando Return.annualized( ) podemos encontrar el rendimiento promedio anual:

sp500_mean_ret <- Return.annualized(sp500_monthly_rets)

Y vemos que este es de 8.68% anual. Aunque estas son medidas ex-post, generalmente son usadas como proxies de los valores ex-ante en procesos que necesiten predicciones sobre retornos en el futuro.

2.1.2 Rendimiento a través del tiempo

Sin embargo, como bien sabemos, este rendimiento no es constante a través del tiempo. Existen periodos de altos rendimientos y de rendimientos negativos. Si quisieramos analizar esta métrica a través del tiempo, podemos usar el siguiente comando:

chart.RollingPerformance(R = sp500_monthly_rets,
    width = 12,
    FUN = "Return.annualized",
    main = "Comportamiento del rendimiento anual del S&P 500")

Rendimiento anual del S&P 500 a través del tiempo.

Lo que estamos haciendo con esta función es selecionando periodos de 12 meses (esto lo controlamos con el parámetro width), aplicando a esta selección la función Return.annualized( ) (esto lo controlamos con el parámetro FUN) y graficando los resultados. Podemos ver claramente los periodos de bajos rendimientos como la burbuja del dot-com a principios del siglo XXI y la crisis financiera del 2008. En estos periodos el S&P 500 tuvo rendimientos de -20% y -40%. No todo ha sido ganancias constantes incluso con el índice más popular del mundo.

2.1.3 La distribución de los retornos

La teoría moderna de portafolios es la base de los últimos avances en finanzas (nosotros vamos a ver varios de estos avances en tutoriales posteriores), pero tiene muchas críticas válidas sobre sus cimientos. Una de las más importantes es que asume que los retornos de los activos siguen una distribución normal. Analicemos esta suposición para los retornos del S&P 500.

Como vimos anteriormente para el caso de una sola acción, podemos hacer esto de manera visual:

Análisis visual de normalidad de los retornos mensuales del S&P 500.

Vemos una distribución no simétrica, con skewness negativo. Las colas de la distribución se ven muy grandes, lo que indica también exceso de curtosis. Esto podemos comprobarlo con las siguientes funciones:

skewness(sp500_monthly_rets)
kurtosis(sp500_monthly_rets)

Y comprobamos que efectivamente tenemos skewness negativo de -0.58 y 1.29 de exceso de curtosis. Aunque la distribución normal no se sigue al pie de la letra, es costumbre asumir que este es el caso puesto que la desviación estándar tiende a ser una buena medida de escala. Si quieres leer más sobre este tema, te recomiendo este artículo.

2.2 Riesgo del portafolio

Anteriormente ya exploramos el riesgo de una acción. Todas esas medidas son válidas para portafolios y serían medidas ex-post del riesgo de un portafolio. En este tutorial vamos a concentrarnos en cómo calcular la varianza ex-ante de un portafolio.

La varianza ex-ante de un portafolio de dos activos, como nuestra estrategia buy and hold, está dada por:

var(P) = w_1^2*var(R_1) + w_2^2*var(R_2) + 2*w_1*w_2*cov(R_1, R_2)

donde w_1: peso del activo 1
      w_2: peso del activo 2
      R_1: retornos del activo 1
      R_2: retornos del activo 2
      var: función de varianza
      cov: función de covarianza

Para un portafolio de 3 activos, sería:

var(P) = w_1^2*var(R_1) + w_2^2*var(R_2) + w_3^2*var(R_3) + 2*w_1*w_2*cov(R_1, R_2) + 2*w_1*w_3*cov(R_1, R_3) + 2*w_2*w_3*cov(R_2, R_3)

donde w_1: peso del activo 1
      w_2: peso del activo 2
      w_3: peso del activo 3
      R_1: retornos del activo 1
      R_2: retornos del activo 2
      R_3: retornos del activo 3
      var: función de varianza
      cov: función de covarianza

Para un portafolio de ~500 activos como el S&P 500, estamos hablando de una ecuación con más de 125,000 términos. Como podrán imaginarse, es un tanto impráctico calcularla de esta manera. En vez de eso, utilizamos notación matricial:

var(P) = w'Sw

donde w: vector de pesos del portafolio
      S: matriz de covarianza

La matriz de covarianza es simplemente una matriz de la siguiente forma:

Matriz de covarianza.

Donde en la diagonal tenemos la varianza de cada activo y en el término cruzado ij tenemos la covarianza del activo i y el activo j. Comprobemos que estas dos medidas son equivalentes en R:

var_1 = weights[1]^2*var(adj_rets[,1]) + weights[2]^2*var(adj_rets[,2]) + 2*weights[1]*weights[2]*cov(adj_rets)[2]
var_2 = weights %*% cov(adj_rets) %*% t(t(weights))

Ambos métodos dan el mismo resultado: 0.00006265 de varianza ex-ante diaria. O sea que la desviación estándar anualizada ex-ante de nuestro portafolio es de 12.56% (recuerda que para anualizar la desviación estándar hay que multiplicar por la raíz de la periodicidad de los retornos). Esta desviación estándar esperada es consistente con la que hemos observado hasta ahora en la estrategia buy and hold si usamos la función StdDev.annualized( ).

De manera análoga, podremos construir matrices de semivarianza si prefieren usar otras medidas de riesgo como las que ya vimos en el tutorial anterior de riesgo. Estas matrices de covarianza serán muy útiles en tutoriales posteriores cuando cubramos optimización de portafolios.

Igual que en el último tema de la sección anterior, podemos ver que la volatilidad en los retornos no es constante sino que existen periodos de baja y alta volatilidad:

chart.TimeSeries(Return.calculate(sp500), main="Volatilidad en los retornos diarios del S&P 500")

La volatilidad del S&P 500 no es constante.

Intenta crear una gráfica similar a la que hicimos para los retornos donde muestres la desviación estándar de los últimos 12 retornos mensuales a lo largo del tiempo. ¿Puedes identificar los periodos de alta volatilidad? ¿Hubo algún suceso importante en estas fechas?

2.3 Relación entre riesgo y retorno

Cómo bien es sabido, existe una relación teórica entre el riesgo de una inversión y su retorno esperado: a mayor riesgo, se espera mayor retorno. Para poder medir la proporción entre riesgo y retorno, utilizamos el índice Sharpe, que está definido de la siguiente manera:

S = (R - R_f) / s

donde R  : retorno del portafolio o activo
      R_f: tasa libre de riesgo
      s  : volatilidad del portafolio o activo

Y representa la cantidad de retorno que estamos recibiendo por unidad de riesgo. PerformanceAnalytics tiene una función que nos ayuda a calcularlo, SharpeRatio( ):

SharpeRatio(buy_and_hold)

Y nos entrega 3 índices diferentes dependiendo de la medida de riesgo que querramos utilizar: desviación estándar, VaR, o CVaR. De igual manera puedes calcularlo anualizado y hacer una gráfica de cómo ha variado este parámetro a través del tiempo.

Hasta el próximo tutorial!