Intro
En este tutorial vamos a cubrir lo siguiente:
El paquete
PortfolioAnalyticsBacktesting del MSR
Backtesting del GMV
Comparación vs. otros esquemas de construcción de portafolios
1. El paquete PortfolioAnalytics
PortfolioAnalytics es un paquete de R que nos permite hacer optimización de portafolios con distintos objetivos, restricciones y periodos de rebalanceo. El paquete funciona de la siguiente manera:
Se le especifica en un objeto
portfoliolos activos que vamos a utilizar para la optimización.Se le especifica, en el mismo objeto, las restricciones que tiene nuestra optimización (long only, inversión completa, máximos y mínimos de peso para los activos, etc.).
Se le especifica, en el mismo objeto, los objetivos de la optimización (maximizar retorno, minimizar riesgo, etc.).
Se corre la optimización usando la función
optimize.portfolio().
Veamos a continuación cada uno de estos pasos. Antes de todo esto, tenemos que bajar los datos necesarios usando quantmod, como siempre:
# 0. Limpiar la sesión
rm(list=ls())
if (names(dev.cur()) != "null device") {
dev.off()
}
cat("\014")
# 1. Cargar librerías
library(quantmod)
library(PortfolioAnalytics)
library(PerformanceAnalytics)
# 2. Descargar datos y extraer precios ajustados
etf_data <- new.env()
etfs <- c("VOX", "VCR", "VDC", "VDE", "VFH", "VHT", "VIS", "VGT", "VAW", "VNQ", "VPU")
getSymbols(etfs, env = etf_data, from = "2011-11-19", to = "2021-11-19")
adj_list <- lapply(etf_data, Ad)
adj_ts <- do.call(merge, adj_list)
names(adj_ts) <- gsub(".Adjusted", "", names(adj_ts))
# 3. Calcular retornos mensuales
adj_ts <- adj_ts[endpoints(adj_ts, on = "months")]
adj_rets <- na.omit(Return.calculate(adj_ts))1.1 Especificación del portafolio
Lo único que tenemos que hacer aquí es especificarle cuáles son los activos que vamos a utilizar para esta optimización. Hay varias maneras de hacer esto, a mi me gusta usar lo siguiente:
# 4. Configurar el portafolio (MSR = Maximum Sharpe Ratio)
msr_port_spec <- portfolio.spec(assets = names(adj_rets))Voy a llamar este portafolio msr_port_spec por que quiero resolver para el portafolio con máximo índice Sharpe. Les recomiendo siempre usar nombres de variables lo suficientemente descriptivos para que puedan entender lo que están haciendo cuando vuelvan a leer su código meses o años después. Y usen comentarios también.
1.2 Especificación de restricciones
Existen muchas restricciones que podemos usar en nuestro portafolio. Hoy vamos a ver sólo estas dos, aunque en tutoriales posteriores cubriremos más:
# 5. Especificar las restricciones del problema
msr_port_spec <- add.constraint(portfolio = msr_port_spec, type = "full_investment")
msr_port_spec <- add.constraint(portfolio = msr_port_spec, type = "long_only")Aquí le estamos diciendo PortfolioAnalytics que queremos dos cosas: los pesos deben sumar 100% (eso es lo que significa full_investment) y los pesos deben ser positivos (eso es lo que significa long_only). No vamos a contemplar ventas en corto ni apalancamiento para esta optimización.
1.3 Especificación de los objetivos
Aquí le especificamos a PortfolioAnalytics qué es lo que estamos buscando con esta optimización:
# 6. Especificar los objetivos del problema
msr_port_spec <- add.objective(portfolio = msr_port_spec, type = "return", name = "mean")
msr_port_spec <- add.objective(portfolio = msr_port_spec, type = "risk", name = "StdDev")Los objetivos de tipo return son métricas que buscamos maximizar. Los objetivos de tipo risk son métricas que buscamos minimizar. Con estas dos líneas le decimos que queremos maximizar el retorno de nuestro portafolio, usando la función mean, y queremos minimizar el riesgo del portafolio también, usando la función StdDev. Esta última función es la misma del paquete PerformanceAnalytics, el cual venimos usando desde hace rato. PortfolioAnalytics fue diseñado desde el principio para apalancarse sobre el paquete de PerformanceAnalytics. Esto nos va a simplificar muchas cosas que vamos a ver en tutoriales posteriores.
1.4 Correr la optimización
Ahora lo único que falta es resolver nuestro problema de optimización:
# 5. Resolver el problema de optimización
opt <- optimize.portfolio(R = adj_rets,
portfolio = msr_port_spec,
optimize_method = "ROI",
maxSR = TRUE) Aquí le especificamos a PortfolioAnalytics los retornos de nuestros activos (R = adj_rets), el problema que queremos resolver (portfolio = msr_port_spec), el método a utilizar (optimize_method = “ROI”) y que queremos encontrar el portafolio con el máximo índice Sharpe (maxSR = TRUE). Existen muchas más opciones que podemos ajustar y métodos que podemos utilizar, pero por este tutorial esto será suficiente, luego veremos problemas más complicados que nos obliguen a usar otros métodos y ajustes de esta función.
1.5 Análisis de los resultados
El objeto opt es una lista que contiene 9 elementos donde especifica diferentes elementos de la optimización: las restricciones, el tiempo que tardo, los pesos calculados, etc. Por ahora investiguemos los pesos que nos darían el máximo índice Sharpe:
# 6. Análisis de los resultados
chart.Weights(opt, main = "Pesos del MSR")Podemos ver los límites de los valores que pueden tomar los pesos en las líneas grises y los valaores que toman al resolverse la optimización en la línea azul. PerformanceAnalytics nos dice que el portafolio con mayor índice Sharpe está compuesto de la siguiente manera: 27.73% en VPU, 46.80% en VGT y 25.47% en VHT.
2. Backtesting del MSR
En el tutorial anterior vimos como el MSR calculado a finales del 2016 tenía menor índice Sharpe que otro esquema de pesos muy simple que no requería muchos cálculos: dar el mismo porcentaje en el portafolio a los 11 ETFs. Sin embargo, esa no fue una comparación muy justa. Lo más justo sería que ese MSR fuera recalculado cada cierto periodo con la información más reciente y el portafolio se rebalanceara para tomar estos pesos. Vamos a hacer justo eso ahora con la ayuda de la función optimize.portfolio.rebalancing():
# 0. Limpiar la sesión
rm(list=ls())
if (names(dev.cur()) != "null device") {
dev.off()
}
cat("\014")
# 1. Cargar librerías
library(quantmod)
library(PortfolioAnalytics)
library(PerformanceAnalytics)
# 2. Descargar datos y extraer precios ajustados
etf_data <- new.env()
etfs <- c("VOX", "VCR", "VDC", "VDE", "VFH", "VHT", "VIS", "VGT", "VAW", "VNQ", "VPU")
getSymbols(etfs, env = etf_data, from = "2011-11-19", to = "2021-11-19")
adj_list <- lapply(etf_data, Ad)
adj_ts <- do.call(merge, adj_list)
names(adj_ts) <- gsub(".Adjusted", "", names(adj_ts))
# 3. Calcular retornos mensuales
adj_ts <- adj_ts[endpoints(adj_ts, on = "months")]
adj_rets <- na.omit(Return.calculate(adj_ts))
# 4. Configurar el portafolio y el caso a optimizar (MSR)
msr_port_spec <- portfolio.spec(assets = names(adj_rets))
msr_port_spec <- add.constraint(portfolio = msr_port_spec, type = "full_investment")
msr_port_spec <- add.constraint(portfolio = msr_port_spec, type = "long_only")
msr_port_spec <- add.objective(portfolio = msr_port_spec, type = "return", name = "mean")
msr_port_spec <- add.objective(portfolio = msr_port_spec, type = "risk", name = "StdDev")
# 5. Configurar el backtesting de nuestro esquema de optimización
msr_opt <- optimize.portfolio.rebalancing(R = adj_rets,
portfolio = msr_port_spec,
optimize_method = "ROI",
maxSR = TRUE,
rebalance_on = "months",
training_period = 61,
rolling_window = 60)
# 6. Analizar el rendimiento de esta estrategia
msr_rets <- Return.portfolio(adj_rets, weights = extractWeights(msr_opt))
names(msr_rets) <- "MaxSharpeRatio"
charts.PerformanceSummary(msr_rets)
chart.Weights(msr_opt, main = "Pesos del MSR")
print(table.AnnualizedReturns(msr_rets))Hasta el punto 4, estamos haciendo lo mismo que hicimos en la sección anterior: bajamos datos necesarios, creamos un portafolio y definimos un problema de optimización con restricciones y objetivos. En el punto 5, estamos llevando a cabo una optimización que se recalcula cada mes (rebalance_on = “months”) y cuyo periodo de entrenamiento es de 61 meses y su ventana de optimización es de 60 meses. Esto quiere decir que la primer optimización va a suceder en el 2016-12-30 (61 meses después del primer dato de noviembre del 2011) y cada que se rebalancee se usarán los últimos 60 retornos (5 años puesto que estamos usando retornos mensuales) para recalcular el portafolio de mayor índice Sharpe. Esto nos da mucho mejores resultados que lo que habíamos visto en el tutorial anterior, donde sólo lo calculábamos una vez y no nos volvíamos a preocupar por recalcularlo. Ahora tenemos un índice Sharpe anualizado de 1.45 comparado con el 0.75 que vimos anteriormente.
Los pesos del MSR cambian a través del tiempo de la siguiente manera:
3. Backtesting del GMV
Con el portafolio de mínima varianza haremos lo mismo, vamos a rebalancearlo periódicamente en vez de elegir pesos al principio y nunca más volver a rebalancear:
# 7. Configurar el portafolio y el caso a optimizar (GMV)
gmv_port_spec <- portfolio.spec(assets = names(adj_rets))
gmv_port_spec <- add.constraint(portfolio = gmv_port_spec, type = "full_investment")
gmv_port_spec <- add.constraint(portfolio = gmv_port_spec, type = "long_only")
gmv_port_spec <- add.objective(portfolio = gmv_port_spec, type = "risk", name = "StdDev")
# 8. Configurar el backtesting de nuestro esquema de optimización
gmv_opt <- optimize.portfolio.rebalancing(R = adj_rets,
portfolio = gmv_port_spec,
optimize_method = "ROI",
rebalance_on = "months",
training_period = 61,
rolling_window = 60)
# 9. Analizar el rendimiento de esta estrategia
gmv_rets <- Return.portfolio(adj_rets, weights = extractWeights(gmv_opt))
names(gmv_rets) <- "GlobalMinVar"
rets <- cbind(msr_rets, gmv_rets)
charts.PerformanceSummary(rets, main = "MSR vs. GMV")
chart.Weights(gmv_opt, main = "Pesos del GMV")
print(table.AnnualizedReturns(rets))Aunque este portafolio tiene peor rendimiento que el MSR, recordemos que ese no es su objetivo. El objetivo de esta optimización es minimizar el riesgo del portafolio (la desviación estándar de sus retornos). Este objetivo se logra, teniendo una desviación estándar anualizada de tan sólo 12.28% (vs. 14.07% para el MSR, por ejemplo).
Los pesos del GMV cambian a través del tiempo de la siguiente manera:
4. Comparación vs. otros esquemas de construcción de portafolios
Otros dos esquemas muy comunes son los siguientes: mismos pesos (ya vimos este tipo de esquemas en el tutorial anterior) y cap-weighted. El esquema cap-weighted consiste en utilizar la capitalización de mercado de cada activo y asignarle su peso en el portafolio de acuerdo a la proporción que representa del total de la capitalización de la muestra. Este es el esquema que se usa para construir, por ejemplo, el S&P 500 y el Russell 2000 en EUA, el IPC en México, el ACWI a nivel global, etc. Para esto, necesitamos conocer la capitalización de mercado de todas las compañías que pertenecen a cada uno de los 11 sectores de la economía representados por nuestros ETFs.
Por suerte para nosotros, ya que no tengo estos datos, podemos utilizar el ETF VTI como proxy. Este ETF sigue un índice cap-weighted de todo el mercado accionario de EUA, así que eso nos garantiza ser equivalente a hacer un cap-weighting de los 11 sectores que estamos utilizando. Generalmente vamos a usar este ETF como benchmark así que lo llamaremos bmk en nuestro script. Veamos la comparación con estos esquemas a continuación:
# 10. Analizar el rendimiento de estas estrategias vs. Mismos Pesos
mismos_pesos <- rep(1/ncol(adj_rets), ncol(adj_rets))
mp_rets <- Return.portfolio(adj_rets["2017-01-31/"], weights = mismos_pesos, rebalance_on = "months")
names(mp_rets) <- "MismosPesos"
rets <- cbind(rets, mp_rets)
charts.PerformanceSummary(rets, main = "MSR vs. GMV vs. Mismos Pesos")
print(table.AnnualizedReturns(rets))
# 11. Analizar el rendimiento de estas estrategias vs. benchmark
bmk <- getSymbols("VTI", from = "2011-11-19", to = "2021-11-19", auto.assign = FALSE)
bmk_ts <- Ad(bmk)
bmk_ts <- bmk_ts[endpoints(bmk_ts, on = "months")]
bmk_rets <- na.omit(Return.calculate(bmk_ts))
names(bmk_rets) <- "BMK"
rets <- cbind(rets, bmk_rets["2017-01-31/"])
charts.PerformanceSummary(rets, main = "MSR vs. GMV vs. Mismos Pesos vs. BMK")
print(table.AnnualizedReturns(rets))Vemos que nuestros esquemas de optimización ahora sí cumplen con sus objetivos. Efectivamente el MSR es el que mayor índice Sharpe nos proporciona y el GMV nos proporciona la opción de menor volatilidad:
En el próximo tutorial cubriremos más restricciones y objetivos que podemos utilizar con este paquete. Hasta el próximo tutorial!





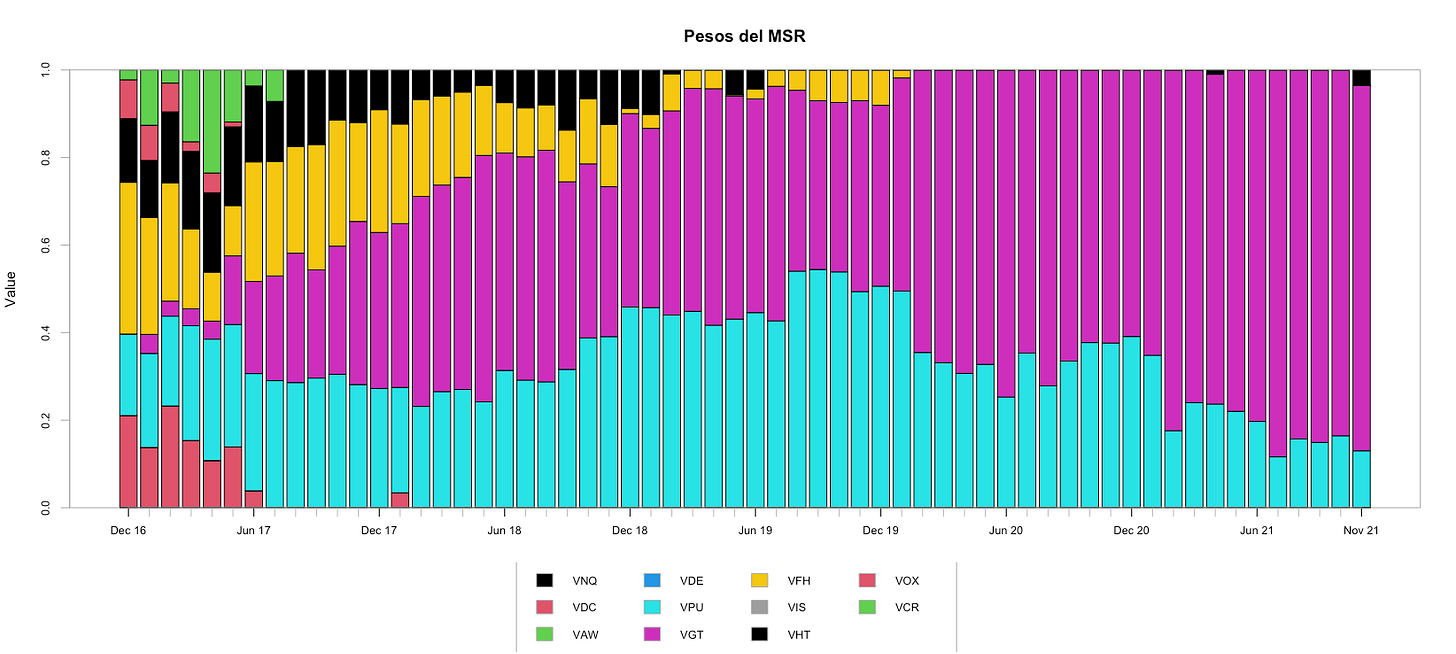




Existe un problema al correr el código en r, este se presenta en la linea: "chart.Weights(msr_opt, main = "Pesos del MSR")"
El error es el siguiente:
Warning: Recycling array of length 1 in vector-array arithmetic is deprecated.
Use c() or as.vector() instead.
Warning: Recycling array of length 1 in array-vector arithmetic is deprecated.
Use c() or as.vector() instead.
Error in `[.xts`(w, row, column) : subscript out of bounds
Seria de gran ayuda una actualización al código, muchas gracias.