Optimización de portafolios en R: Parte 3

Diferentes restricciones, momentos y objetivos

Dec 02, 2021

Intro

En este tutorial vamos a cubrir lo siguiente:

Restricciones disponibles en PortfolioAnalytics
Usando nuestras propias funciones para los momentos de la optimización
Diferentes objetivos disponibles en PortfolioAnalytics

1. Restricciones disponibles en `PortfolioAnalytics`

En el tutorial pasado vimos varias funcionalidades del paquete PortfolioAnalytics para optimización de portafolios. Sin embargo, concluimos que los portafolios que el optimizador arrojaba no eran inversiones sensatas. Los portafolios que arroja este proceso eran muy concentrados. Todo esto puede resolverse con las restricciones disponibles en el mismo paquete. Antes de todo esto, como ya hemos hecho en varios tutoriales, hay que bajar los datos necesarios para nuestro análisis:

# 0. Limpiar la sesión
rm(list=ls())
if (names(dev.cur()) != "null device") {
  dev.off()
}
cat("\014")

# 1. Cargar librerías
# library(quantmod)
library(PortfolioAnalytics)
library(PerformanceAnalytics)
library(MASS)

# 2. Descargar datos y extraer precios ajustados
etf_data <- new.env()
etfs <- c("VOX", "VCR", "VDC", "VDE", "VFH", "VHT", "VIS", "VGT", "VAW", "VNQ", "VPU")
getSymbols(etfs, env = etf_data, from = "2011-11-19", to = "2021-11-19")
adj_list <- lapply(etf_data, Ad)
adj_ts <- do.call(merge, adj_list)
names(adj_ts) <- gsub(".Adjusted", "", names(adj_ts))

# 3. Calcular retornos mensuales
adj_ts <- adj_ts[endpoints(adj_ts, on = "months")]
adj_rets <- na.omit(Return.calculate(adj_ts))

Empecemos ahora sí a agregar restricciones de concentración a nuestros portafolios.

1.1 Restricciones de caja, grupo y posición

Las restricciones de caja nos permiten señalar rangos de pesos permitidos para nuestros activos. Las restricciones de grupo nos permiten señalar máximos y mínimos de peso permitidos para grupos de activos, en vez de rangos individuales para cada uno. Las restricciones de posición nos permiten decirle al optimizador el máximo de elementos que queremos en nuestro portafolio; es decir, nuestro universo de inversión son los 11 ETFs que ya definimos, pero igual y queremos que nuestro portafolio sólo tenga 6 o 7 máximo por que no queremos tener que estar administrando 11 posiciones diferentes. A esta escala tal vez no suene muy complicado administrar un portafolio con 11 posiciones, pero cuando estamos trabajando con universos de 500 o más acciones igual y queremos limitar el número de posiciones a 100 para simplificar nuestro trabajo.

Vamos a fijar a continuación un portafolio base y a partir de ese vamos a agregar restricciones según sea el caso necesario:

# 4. Configurar el portafolio y el caso base a optimizar (MSR)
base_case <- portfolio.spec(assets = names(adj_rets))
base_case <- add.constraint(portfolio = base_case, type = "full_investment")
base_case <- add.constraint(portfolio = base_case, type = "long_only")
base_case <- add.objective(portfolio = base_case, type = "return", name = "mean")
base_case <- add.objective(portfolio = base_case, type = "risk", name = "StdDev")

# 5. Diferentes restricciones

# Restricción de caja
box_case <- add.constraint(portfolio = base_case, type = "box", min = 0.0, max = 0.35)

# Restricción de grupo
# Cyclical ETFs:
#   Consumer Discretionary: VCR
#   Financials: VFH
#   Industrials: VIS
#   IT: VGT
#   Materials: VAW
#   Real Estate: VNQ
# Degensive ETFs:
#   Consumer Staples: VDC
#   Energy: VDE
#   Healthcare: VHT
#   Telecommunication Services: VOX
#   Utilities: VPU
cyclical_etfs <- c("VCR", "VFH", "VIS", "VGT", "VAW", "VNQ")
defensive_etfs <- c("VDC", "VDE", "VHT", "VOX", "VPU")

group_list <- list(cyclical = match(cyclical_etfs, names(adj_rets)), defensive = match(defensive_etfs, names(adj_rets)))

group_case <- add.constraint(portfolio = base_case, type = "group", groups = group_list, group_min = 0.0, group_max = 0.6)

# Restricción de grupo y caja
box_group_case <- add.constraint(portfolio = base_case, type = "box", min = 0.0, max = 0.35)
box_group_case <- add.constraint(portfolio = box_group_case, type = "group",  groups = group_list, group_min = 0.0, group_max = 0.6)

# Restricción de límite de posición
pos_case <- add.constraint(portfolio = base_case, type = "weight_sum", min_sun = 0.99, max_sum = 1.01)
pos_case <- add.constraint(portfolio = pos_case, type = "position_limit", max_pos = 5)

Creamos aquí 4 casos diferentes. El primero es box_case, donde limitamos el peso de cualquier ETF en nuestro portafolio a máximo 35%. El segundo es group_case, donde creamos dos grupos: uno con los ETFs de las industrias cíclicas y otro con las defensivas, y limitamos el peso de cada grupo a máximo 60% del portafolio. Aquí está permitido que un sólo ETF tome ese 60% o el 40% restante sin problema (e.g. VGT puede ser el 60% del portafolio y no estaríamos rompiendo la restricción puesta). Para esto creamos el tercer caso, box_group_case, donde limitamos las posiciones individuales a 35% y aparte limitamos el peso de cualquiera de los dos grupos a 60%. Por último, en pos_case limitamos el número de ETFs en nuestro portafolio a un máximo de 5.

Todos estas restricciones pueden combinarse y ser modificadas. Entren a la página del paquete para que vean de qué manera pueden modificar estas restricciones y cuáles otras pueden incluir en sus optimizaciones.

A continuación vamos a correr cada uno de estos casos como hicimos anteriormente y vamos a analizar varias cosas:

# 6. Configurar el backtesting de nuestros esquemas de optimización
msr_opt <- optimize.portfolio.rebalancing(R = adj_rets,
                                          portfolio = base_case,
                                          optimize_method = "ROI",
                                          maxSR = TRUE,  
                                          rebalance_on = "quarters",
                                          training_period = 61,
                                          rolling_window = 60)

box_opt <- optimize.portfolio.rebalancing(R = adj_rets,
                                          portfolio = box_case,
                                          optimize_method = "ROI",
                                          maxSR = TRUE,  
                                          rebalance_on = "quarters",
                                          training_period = 61,
                                          rolling_window = 60)

grp_opt <- optimize.portfolio.rebalancing(R = adj_rets,
                                          portfolio = group_case,
                                          optimize_method = "ROI",
                                          maxSR = TRUE,  
                                          rebalance_on = "quarters",
                                          training_period = 61,
                                          rolling_window = 60)

bng_opt <- optimize.portfolio.rebalancing(R = adj_rets,
                                          portfolio = box_group_case,
                                          optimize_method = "ROI",
                                          maxSR = TRUE,  
                                          rebalance_on = "quarters",
                                          training_period = 61,
                                          rolling_window = 60)

pos_opt <- optimize.portfolio.rebalancing(R = adj_rets,
                                          portfolio = pos_case,
                                          optimize_method = "random",
                                          maxSR = TRUE,
                                          search_size = 1000,
                                          rebalance_on = "quarters",
                                          training_period = 61,
                                          rolling_window = 60)

# 7. Analizar el rendimiento de estas estrategias
msr_rets <- Return.portfolio(adj_rets, weights = extractWeights(msr_opt))
box_rets <- Return.portfolio(adj_rets, weights = extractWeights(box_opt))
grp_rets <- Return.portfolio(adj_rets, weights = extractWeights(grp_opt))
bng_rets <- Return.portfolio(adj_rets, weights = extractWeights(bng_opt))
# Ajustar pesos del caso "pos"
pos_weights <- extractWeights(pos_opt)
pos_weights <- pos_weights/rowSums(pos_weights)
pos_rets <- Return.portfolio(adj_rets, weights = pos_weights)
names(msr_rets) <- "MaxSharpeRatio"
names(box_rets) <- "RestrCaja"
names(grp_rets) <- "RestrGrupo"
names(bng_rets) <- "RestrCajaYGrupo"
names(pos_rets) <- "RestrPosicion"
rets <- cbind(msr_rets, box_rets, grp_rets, bng_rets, pos_rets)
print(chart.CumReturns(rets, main = "Diferentes Restricciones",
                       legend.loc = "topleft"))
chart.Weights(msr_opt, main = "Pesos del MSR")
chart.Weights(box_opt, main = "Pesos del MSR con Restricción de Caja")
chart.Weights(grp_opt, main = "Pesos del MSR con Restricción de Grupo")
chart.Weights(bng_opt, main = "Pesos del MSR con Restricción de Caja y Grupo")
chart.Weights(pos_opt, main = "Pesos del MSR con Restricción de Posición")
print(table.AnnualizedReturns(rets))

# 8. Confirmar que se respetan los pesos de los grupos
msr_weight_history <- extractWeights(msr_opt)
msr_weight_history$Cyclical <- rowSums(msr_weight_history[, cyclical_etfs])
msr_weight_history$Defensive <- rowSums(msr_weight_history[, defensive_etfs])
chart.StackedBar(msr_weight_history[, c("Cyclical", "Defensive")],
                 main = "Pesos de los grupos en el MSR")
box_weight_history <- extractWeights(box_opt)
box_weight_history$Cyclical <- rowSums(box_weight_history[, cyclical_etfs])
box_weight_history$Defensive <- rowSums(box_weight_history[, defensive_etfs])
chart.StackedBar(box_weight_history[, c("Cyclical", "Defensive")],
                 main = "Pesos de los grupos en el MSR con Restricción de Caja")
grp_weight_history <- extractWeights(grp_opt)
grp_weight_history$Cyclical <- rowSums(grp_weight_history[, cyclical_etfs])
grp_weight_history$Defensive <- rowSums(grp_weight_history[, defensive_etfs])
chart.StackedBar(grp_weight_history[, c("Cyclical", "Defensive")],
                 main = "Pesos de los grupos en el MSR con Restricción de Grupo")
bng_weight_history <- extractWeights(bng_opt)
bng_weight_history$Cyclical <- rowSums(bng_weight_history[, cyclical_etfs])
bng_weight_history$Defensive <- rowSums(bng_weight_history[, defensive_etfs])
chart.StackedBar(bng_weight_history[, c("Cyclical", "Defensive")],
                 main = "Pesos de los grupos en el MSR con Restricción de Caja y Grupo")
pos_weight_history <- extractWeights(pos_opt)
pos_weight_history$Cyclical <- rowSums(pos_weight_history[, cyclical_etfs])
pos_weight_history$Defensive <- rowSums(pos_weight_history[, defensive_etfs])
chart.StackedBar(pos_weight_history[, c("Cyclical", "Defensive")],
                 main = "Pesos de los grupos en el MSR con Restricción de Posición")

# 9. Analizar el rendimiento de estas estrategias vs. benchmark
bmk <- getSymbols("VTI", from = "2011-11-19", to = "2021-11-19",
                  auto.assign = FALSE)
bmk_ts <- Ad(bmk)
names(bmk_ts) <- "BMK"
bmk_ts <- bmk_ts[endpoints(bmk_ts, on = "months")]
bmk_rets <- na.omit(Return.calculate(bmk_ts))
rets <- cbind(rets, bmk_rets["2017-01-31/"])
print(chart.CumReturns(rets, main = "Diferentes Restricciones vs. BMK",
                       legend.loc = "topleft"))
print(table.AnnualizedReturns(rets))

Podemos ver como el caso base sigue siendo un portafolio muy concentrado:

Pero al introducir la restricción de caja obtenemos un portafolio más diversificado por el simple hecho de que ningún ETF puede representar más del 35% del portafolio:

Por otra parte, los portafolios con restricción de grupo siguen el comportamiento esperado. En ningún momento cualquiera de los dos grupos representa más del 60% del portafolio:

Y el último caso, donde tenemos límites de posición, nunca tenemos más de 5 activos en el portafolio, como especificamos al fijar la restricción:

Se darán cuenta que para la última optimización, pos_opt, utilizamos otro método de optimización que para el resto. Esto es debido a que el problema dejó de ser un problema convexo al introducir esta restricción. Es decir, no hay un mínimo (o máximo) global para la función que podamos encontrar de manera cerrada. Esto nos obliga a usar otro optimizador diferente del ROI. Por suerte para nosotros, PortfolioAnalytics tiene varios optimizadores más disponibles para problemas no convexos. random es sólo uno de ellos pero busquen en la documentación del paquete que otras técnicas pueden usar en estos casos.

Después de calcular todas estas diferentes restricciones, vemos que el rendimiento del MSR ha bajado, y un caso resulta ya no ser mejor que el benchmark que habíamos definido anteriormente:

Recordemos que el objetivo es obtener mejor índice Sharpe que el benchmark y no necesariamente ganarle en retorno, así que sólo el caso pos_case es peor que el benchmark aunque tengamos 3 estrategias con retornos menores.

2. Usando nuestras propias funciones para los momentos de la optimización

Para la optimización de portafolios, generalmente usamos los dos primeros momentos estadísticos: el promedio (retorno esperado) y la varianza (riesgo). Por eso en inglés este proceso se comoce como mean-variance optimization. Ya mencionamos anteriormente que otro problema con este método es el hecho de que si nuestros estimados de retorno esperado y varianza son malos, el resultado seguramente será malo (garbage in, garbage out). Vamos a revisar ahora otra función muy útil de PortfolioAnalytics: la capacidad de usar nuestras propias funciones para el cálculo de los momentos utilizados en la optimización.

Después de bajar los datos necesarios, el procedimiento es el siguiente:

# 4. Configurar el portafolio y el caso base a optimizar (GMV)
base_case <- portfolio.spec(assets = names(adj_rets))
base_case <- add.constraint(portfolio = base_case, type = "full_investment")
base_case <- add.constraint(portfolio = base_case, type = "long_only")
base_case <- add.objective(portfolio = base_case, type = "risk", name = "StdDev")

# 5. Definir nuestra propia función de momentos
custom.moments <- function(R, portfolio, rob_method = "mcd") {
  out <- list()
  out$sigma <- cov.rob(R, method = rob_method)$cov
  return(out)
}

# 7. Correr los diferentes esquemas de optimización
gmv_base_opt <- optimize.portfolio.rebalancing(R = adj_rets,
                                               portfolio = base_case,
                                               optimize_method = "ROI",
                                               rebalance_on = "quarters",
                                               training_period = 61,
                                               rolling_window = 60)

gmv_rmcd_opt <- optimize.portfolio.rebalancing(R = adj_rets,
                                               portfolio = base_case,
                                               optimize_method = "ROI",
                                               rebalance_on = "quarters",
                                               training_period = 61,
                                               rolling_window = 60,
                                               momentFUN = "custom.moments")

gmv_rmve_opt <- optimize.portfolio.rebalancing(R = adj_rets,
                                               portfolio = base_case,
                                               optimize_method = "ROI",
                                               rebalance_on = "quarters",
                                               training_period = 61,
                                               rolling_window = 60,
                                               momentFUN = "custom.moments",
                                               rob_method = "mve")

# 7. Analizar el rendimiento de estas estrategias
gmv_base_rets <- Return.portfolio(adj_rets, weights = extractWeights(gmv_base_opt))
gmv_rmcd_rets <- Return.portfolio(adj_rets, weights = extractWeights(gmv_rmcd_opt))
grp_rmve_rets <- Return.portfolio(adj_rets, weights = extractWeights(gmv_rmve_opt))
names(gmv_base_rets) <- "GMV Base"
names(gmv_rmcd_rets) <- "GMV rMCD"
names(grp_rmve_rets) <- "GMV rMVE"
rets <- cbind(gmv_base_rets, gmv_rmcd_rets, grp_rmve_rets)
print(chart.CumReturns(rets, main = "Diferentes Momentos", legend.loc = "topleft"))
print(table.AnnualizedReturns(rets))

Nuestro base_case es una optimización con la que ya estamos familiarizados: buscamos obtener el portafolio de mínima varianza (GMV). En el paso 5 definimos nuestra función de momentos. Esta función siempre debe tener los primeros dos parámetros R (los retornos de los activos de nuestro portafolio) y portfolio. Estos dos serán usados por el paquete en sus cálculos internos así que es mejor incluirlos con ese nombre y en ese orden exactamente para evitar problemas después. La función deberá regresar una lista con los elementos necesarios a modificar. Para este caso sólo necesitamos la matriz de covarianza, pero si piensan modificar los 4 parámetros permitidos aquí les va la lista:

mu: retorno esperado
sigma: matriz de covarianza
m3: skewness
m4: curtosis

Esos nombres debe tener cada elemento de la lista y contener los datos especificados. En nuestro caso nomás necesitamos la matriz de covarianza (no utilizamos ningún otro momento para calcular el GMV) así que sólo necesitamos asegurarnos de especificar el parámetro sigma.

Para nuestro cálculo de matriz de covarianza vamos a utilizar la función cov.rob() del paquete MASS. Esto nos permitirá calcular una matriz de covarianza con cualquiera de los dos métodos disponibles: el método del minimum volume ellipsoid (method = “mve”) y el método del minimum covariance determinant (method = “mcd”).

Cuando corremos la optimización y queremos usar nuestra propia función para calcular los momentos de la optimización, hay que especificarle a PortfolioAnalytics usando el parámetro momentFUN en optimize.portfolio(). Cualquier parámetro extra que queramos especificar, como en nuestro caso el rob_method lo incluímos directamente en la misma función.

Veamos si estimaciones más robustas de la matriz de covarianza resultan en portafolios con menores varianzas:

Aunque ambas estrategias resultan en mayor retorno que el caso base, ambas también tienen mayor volatilidad (que es lo que estabamos buscando reducir). En este caso, debemos concluir que un método más robusto de estimación de la matriz de covarianza no resultó en una mejor optimización del problema. Habrá que probar con más estimadores a ver si existe algún método que sí represente una mejora en este sentido.

3. Diferentes objetivos disponibles en `PortfolioAnalytics`

Ahora vamos a analizar las diferentes funcionalidades que ofrece este paquete con respecto a los objetivos de nuestra optimización. Ya hemos visto los objetivos básicos: maximizar retorno o minimizar riesgo. Ahora veamos dos maneras más de especificarle nuestros objetivos: maximizar la utilidad cuadrática del portafolio y maximizar o minimizar alguna medida que nosotros definamos.

La utilidad cuadrática de un portafolio está dada por la siguiente ecuación:

utilidad = w'R - (𝝀/2)w'𝝨w
donde w: vector de pesos del portafolio
      R: vector de retornos esperados
      𝝀: parámetro de aversión al riesgo
      𝝨: matriz de covarianza de los activos del portafolio

El objetivo es maximizar esta relación. El parámetro de aversión al riesgo es un número arbitrario que nosotros usaremos para definir que tanto nos importa el riesgo. A mayor aversión, menor riesgo tendrá el portafolio que resulte de la optimización.

Veamos a continuación cómo se fijan los diferentes casos de objetivos posibles:

# 4. Configurar el portafolio y el caso base a optimizar
base_case <- portfolio.spec(assets = names(adj_rets))
base_case <- add.constraint(portfolio = base_case, type = "full_investment")
base_case <- add.constraint(portfolio = base_case, type = "long_only")

# 5. Diferentes objetivos

# Maximizar retorno
max_ret_case <- add.objective(portfolio = base_case, type = "return", name = "mean")

# Minimizar riesgo
min_ES_case <- add.objective(portfolio = base_case, type = "risk", name = "ES")

# Maximizar utilidad cuadrática
max_QU_case <- add.objective(portfolio = base_case, type = "quadratic_utility",
                             risk_aversion = 3)

# Maximizar objetivo definido por nosotros
sharpe_ratio <- function(R, weights, sigma, scale, risk_free) {
  ret <- Return.annualized(Return.portfolio(R, weights), scale = scale)
  std_dev <- sqrt(as.numeric(t(weights) %*% sigma %*% weights))*sqrt(scale)
  
  return((ret - risk_free)/std_dev)
}

custom.moments <- function(R, ...) {
  out <- list()
  out$sigma <- cov(R)
  return(out)
}

max_SR_case <- add.constraint(portfolio = base_case, type = "weight_sum",
                              min_sum = 0.99, max_sum = 1.01)
max_SR_case <- add.objective(portfolio = max_SR_case, type = "return",
                             name = "sharpe_ratio",
                             arguments = list(scale = 12, risk_free = 0.01))

# 6. Correr los diferentes esquemas de optimización
max_ret_opt <- optimize.portfolio(R = adj_rets,
                                  portfolio = max_ret_case,
                                  optimize_method = "ROI")

min_ES_opt <- optimize.portfolio(R = adj_rets,
                                 portfolio = min_ES_case,
                                 optimize_method = "ROI")

max_QU_opt <- optimize.portfolio(R = adj_rets,
                                 portfolio = max_QU_case,
                                 optimize_method = "ROI")

max_SR_opt <- optimize.portfolio(R = adj_rets,
                                 portfolio = max_SR_case,
                                 momentFUN = "custom.moments")

# 7. Analizar el resultado de estas optimizaciones
max_ret_rets <- Return.portfolio(R = adj_rets,
                                 weights = extractWeights(max_ret_opt))
names(max_ret_rets) <- "MaxRet"
min_ES_rets <- Return.portfolio(R = adj_rets,
                                weights = extractWeights(min_ES_opt))
names(min_ES_rets) <- "MinES"
max_QU_rets <- Return.portfolio(R = adj_rets,
                                weights = extractWeights(max_QU_opt))
names(max_QU_rets) <- "MaxQU"
# Ajustar pesos del max_SR_opt
max_SR_weights <-  extractWeights(max_SR_opt)
max_SR_weights <- max_SR_weights/sum(max_SR_weights)
max_SR_rets <- Return.portfolio(R = adj_rets,
                                weights = max_SR_weights)
names(max_SR_rets) <- "MaxSR"
rets <- cbind(max_ret_rets, min_ES_rets, max_QU_rets, max_SR_rets)
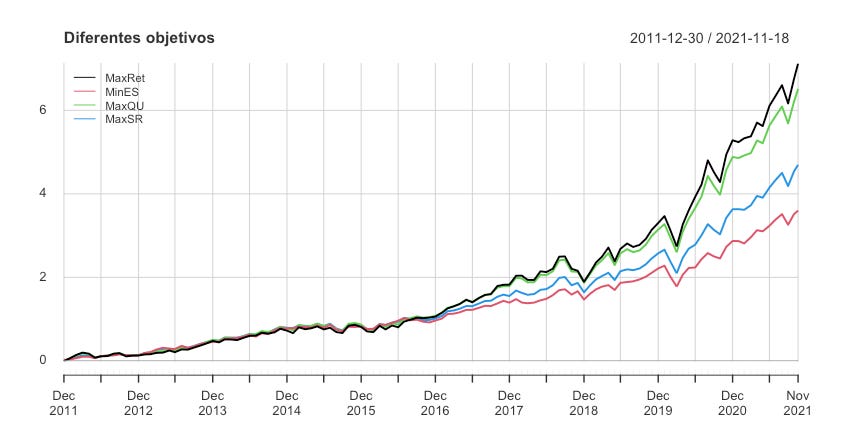
print(chart.CumReturns(rets, legend.loc = "topleft", main = "Diferentes objetivos"))
print(table.AnnualizedReturns(rets))

Aquí tenemos 4 casos. En max_ret_case buscamos simplemente maximizar el retorno esperado del portafolio, sin preocuparnos por el riesgo. Evidentemente esto resultará en tomar una posición del 100% en el ETF con mayor rendimiento histórico hasta ahora, una posición tal vez no muy sensata para el inversionista común. En min_ES_case buscamos minimizar el expected shortfall ( o CVaR) de nuestro portafolio. Ya hemos platicado sobre esta medida de riesgo anteriormente. En max_QU_case vamos a maximizar la utilidad cuadrática, la medida que acabamos de discutir arriba. Por último, en max_SR_case, buscamos maximizar el índice Sharpe del portafolio usando nuestra propia función. Siempre que use mi propia función para mis objetivos tengo que definir los primeros dos parámetros como R y weights y definir una función de momentos para este caso en específico. PortfolioAnalytics va a asumir por default que el objetivo no es convexo, así que necesito usar algún otro método que no sea ROI.

Podemos ver el resultado de este ejercicio a continuación:

Y vemos que todos los objetivos son cumplidos. Tengo un portafolio con máximo retorno, uno con CVaR mínimo y el índice Sharpe del caso con nuestra propia función también es el más grande de los 4. Aquí estamos haciendo un poco de trampa puesto que calculamos los pesos a final del periodo y regresamos a calular estas métricas en el pasado (esto se conoce como look ahead bias) pero sólo estamos haciéndolo con fines ilustrativos.

Por ahora será todo del tema de optimización. Pueden ir a la documentación para revisar todos los demás objetivos, restricciones y maneras de definir momentos que el paquete tiene disponibles, pero son muchas como para cubrir todas en estos tutoriales. Próximamente veremos cómo hacer backtests de estrategias discrecionales que no necesariamente requieran usar optimización de portafolios.

Hasta el próximo tutorial!

mexiquant’s Newsletter

Discussion about this post